Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{4}{3}\\x_1x_2=-\dfrac{1}{3}\end{matrix}\right.\)
\(A=\dfrac{x_1-1}{x_2+1}+\dfrac{x_2-1}{x_1+1}=\dfrac{\left(x_1-1\right)\left(x_1+1\right)+\left(x_2-1\right)\left(x_2+1\right)}{\left(x_2+1\right)\left(x_1+1\right)}\)
\(=\dfrac{x_1^2+x_2^2-2}{x_1x_2+x_1+x_2+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-2}{x_1x_2+x_1+x_2+1}\)
\(=\dfrac{\left(-\dfrac{4}{3}\right)^2-2.\left(-\dfrac{1}{3}\right)-2}{-\dfrac{1}{3}-\dfrac{4}{3}+1}=...\)

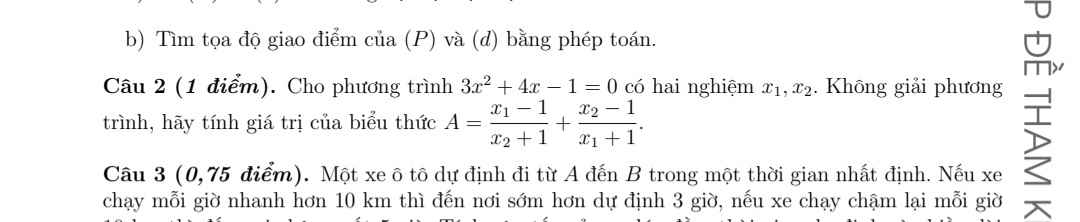
















 Giúp mik câu 3 bài 1 với ạ
Giúp mik câu 3 bài 1 với ạ
