a) \(\text{∆}=\left(2m-1\right)^2-4\left(-m\right)\)
\(=4m^2+1>0\forall m\)
b) Vì phương trình có 2 nghiệm x1, x2 áp dụng hệ thức Vi-ét
\(\left\{{}\begin{matrix}x_1+x_2=-2m+1\\x_1x_2=-m\end{matrix}\right.\)
Ta có:
\(A=x^2_1+x^2_2-6x_1x_2\)
\(=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(-2m+1\right)^2-8.\left(-m\right)\)
\(=4m^2-4m+1+8m\)
\(=\left(2m+1\right)^2\ge0\forall m\)
Min \(A=0\Leftrightarrow m=-\dfrac{1}{2}\)






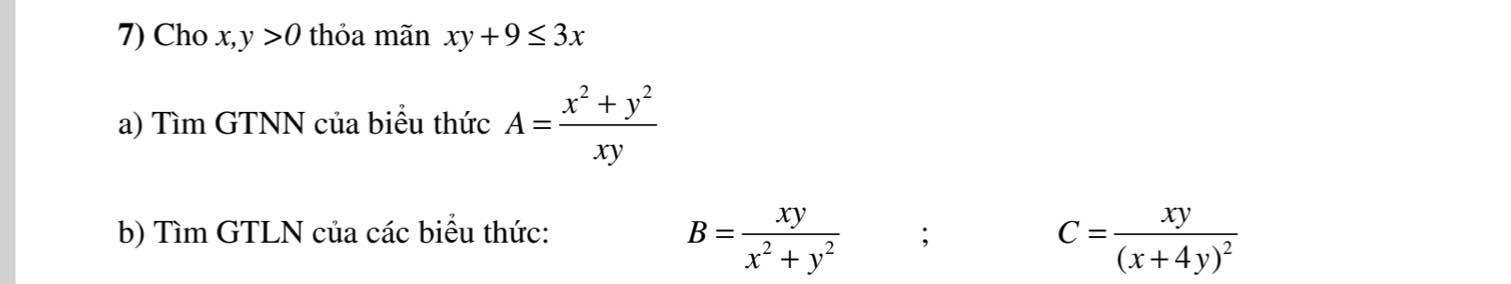 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺