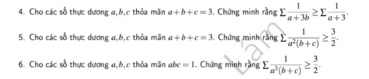4.
\(\dfrac{1}{a+3b}+\dfrac{1}{c+3}\ge\dfrac{4}{a+3b+c+3}=\dfrac{4}{\left(a+b+c\right)+2b+3}=\dfrac{4}{2b+6}=\dfrac{2}{b+3}\)
Tương tự:
\(\dfrac{1}{b+3c}+\dfrac{1}{a+3}\ge\dfrac{2}{c+3}\)
\(\dfrac{1}{c+3a}+\dfrac{1}{b+3}\ge\dfrac{2}{a+3}\)
Cộng vế:
\(\sum\dfrac{1}{a+3b}+\sum\dfrac{1}{a+3}\ge\sum\dfrac{2}{a+3}\)
\(\Rightarrow\sum\dfrac{1}{a+3b}\ge\sum\dfrac{1}{a+3}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)
6.
Đặt \(\left(a;b;c\right)=\left(\dfrac{1}{x};\dfrac{1}{y};\dfrac{1}{z}\right)\Rightarrow xyz=1\)
\(\Rightarrow\sum\dfrac{1}{a^3\left(b+c\right)}=\sum\dfrac{x^3yz}{y+z}=\sum\dfrac{x^2}{y+z}\ge\dfrac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(a=b=c=1\)