Lời giải:
a.
Để pt có 2 nghiệm pb dương thì:
\(\left\{\begin{matrix}
\Delta=(3m-2)^2-4(2m^2-3m+1)>0\\
S=3m-2>0\\
P=2m^2-3m+1>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m^2>0\\
m> \frac{2}{3}\\
(m-1)(2m-1)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ m> \frac{2}{3}\\ \text{m>1 hoặc m}< \frac{1}{2}\end{matrix}\right.\Leftrightarrow m>1\)
b. $\Delta=m^2\geq 0$ nên pt luôn có nghiệm với mọi $m$
Vì $\Delta=m^2$ nên pt có 2 nghiệm
\(\frac{3m-2+m}{2}=2m-1; \frac{3m-2-m}{2}=m-1\)
Nếu $x_1=2m-1, x_2=m-1$ thì:
$x_1^2+x_2=5$
$\Leftrightarrow (2m-1)^2+m-1=5$
$\Leftrightarrow 4m^2-3m-5=0$
$\Leftrightarrow m=\frac{3\pm \sqrt{89}}{8}$
Nếu $x_1=m-1, x_2=2m-1$ thì:
Khi đó:
$x_1^2+x_2=5$
$\Leftrightarrow (m-1)^2+2m-1=5$
$\Leftrightarrow m^2=5$
$\Leftrightarrow m=\pm \sqrt{5}$

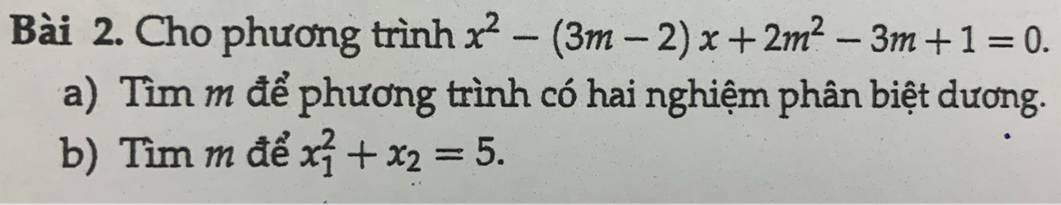 giúp em với
giúp em với




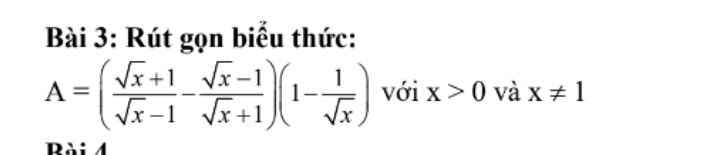








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp


