1.\(m=2\)
\(\Leftrightarrow x^2-2\left(2+1\right)x+3.2-3=0\)
\(\Leftrightarrow x^2-6x+3=0\)
\(\Delta=\left(-6\right)^2-4.3=36-12=24>0\)
=> pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{6+2\sqrt{6}}{2}=3+\sqrt{6}\\x_2=\dfrac{6-2\sqrt{6}}{2}=3-\sqrt{6}\end{matrix}\right.\)
b.Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1.x_2=3m-3\end{matrix}\right.\)
\(\sqrt{x_1-1}+\sqrt{x_2-1}=4\)
\(\Leftrightarrow x_1-1+x_2-1+2\sqrt{\left(x_1-1\right)\left(x_2-1\right)}=16\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2-x_1-x_2+1}=18\)
\(\Leftrightarrow2m+2+2\sqrt{3m-3-\left(2m+2\right)+1}=18\)
\(\Leftrightarrow2m+2\sqrt{m+4}=16\)
\(\Leftrightarrow m+\sqrt{m+4}=8\)
\(\Leftrightarrow\sqrt{m+4}=8-m\)
\(\Leftrightarrow m+4=64-16m+m^2\)
\(\Leftrightarrow m^2-17m+60=0\)
\(\Delta=\left(-17\right)^2-4.60=49>0\)
\(\rightarrow\left\{{}\begin{matrix}x_1=\dfrac{17+\sqrt{49}}{2}=12\\x_2=\dfrac{17-\sqrt{49}}{2}=5\end{matrix}\right.\)
Vậy \(m=12;5\)








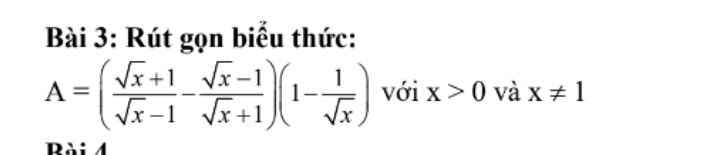








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp


