giúp em với!!!
Bài 2:
b) Ta có: \(N=\dfrac{1}{1\cdot5}+\dfrac{1}{5\cdot10}+\dfrac{1}{10\cdot15}+...+\dfrac{1}{2005\cdot2010}\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{5}{5\cdot10}+\dfrac{5}{10\cdot15}+...+\dfrac{5}{2005\cdot2010}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(1-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+...+\dfrac{1}{2005}-\dfrac{1}{2010}\right)\)
\(=\dfrac{1}{5}+\dfrac{1}{5}\left(1-\dfrac{1}{2010}\right)\)
\(=\dfrac{1}{5}\left(2-\dfrac{1}{2010}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{4019}{2010}=\dfrac{4019}{10050}\)
Đúng 0
Bình luận (0)
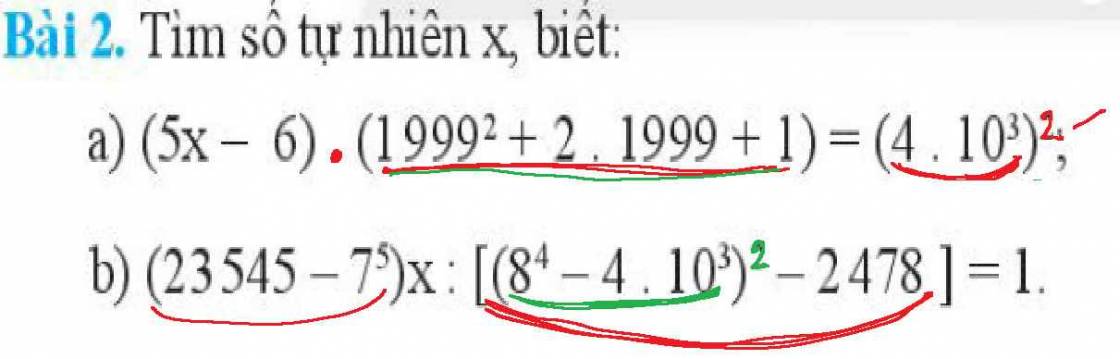
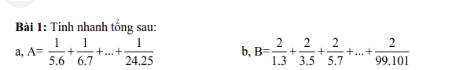
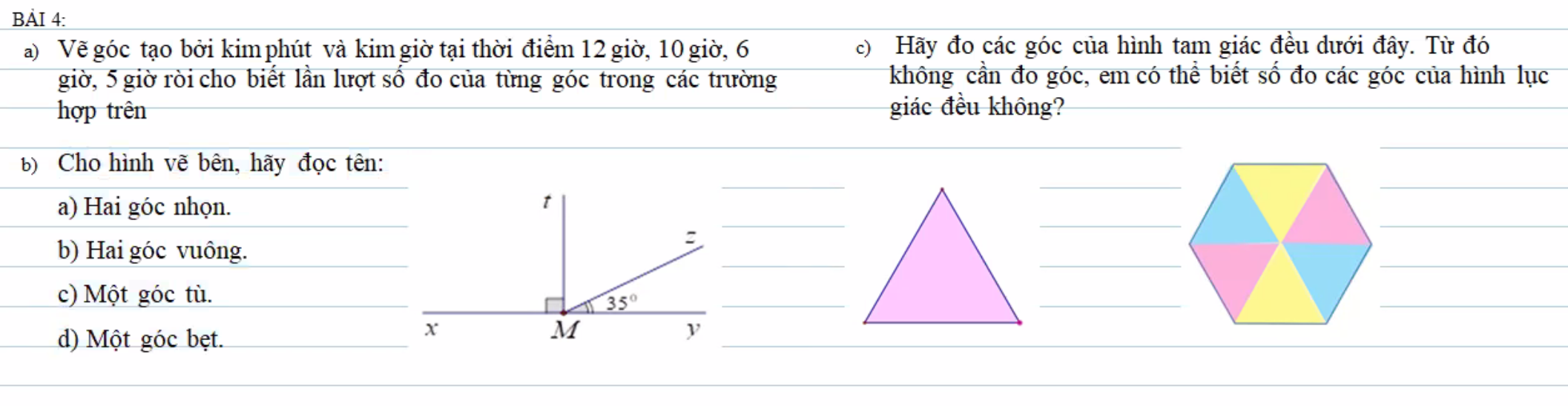
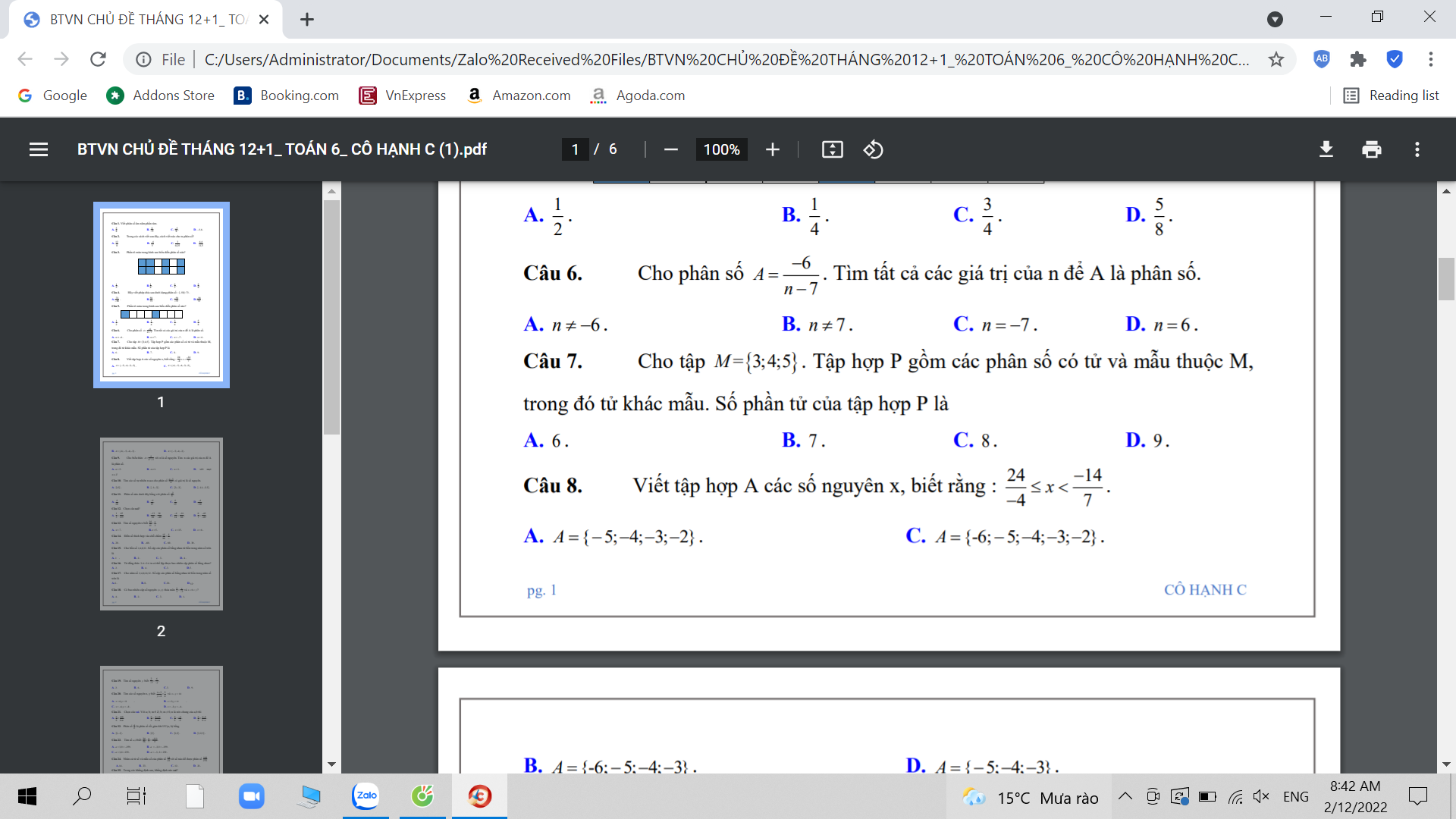mọi người giúp em với ạ em đang cần gấp!!
