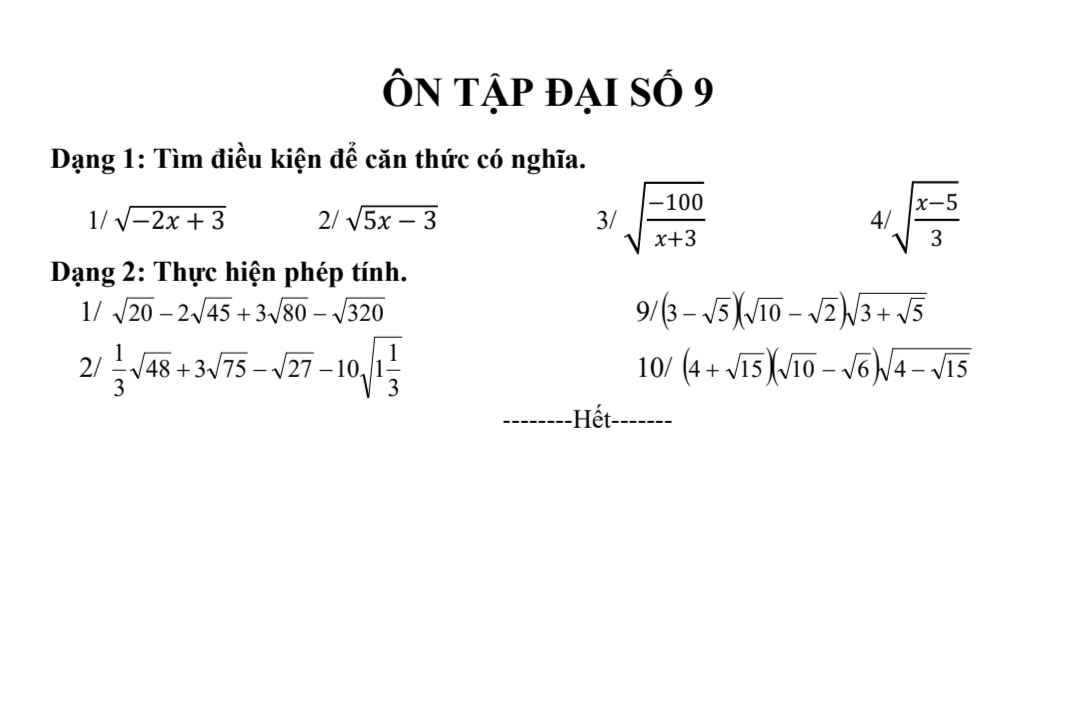
\(a,\) ĐKXĐ: \(x\ge0;x\ne1\)
\(b,\) Khi \(x=0\)
\(\Leftrightarrow A=\dfrac{0-11}{0+0-3}-\dfrac{0-2}{0-1}-\dfrac{0+3}{0+3}\\ \Leftrightarrow A=\dfrac{-11}{-3}-\dfrac{-2}{-1}-\dfrac{3}{3}=\dfrac{11}{3}-2-1=-\dfrac{11}{3}-3=\dfrac{2}{3}\)
\(c,A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}-\dfrac{3\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\\ A=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{15\sqrt{x}-11-3x-7\sqrt{x}+6-2x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{\left(\sqrt{x}-1\right)\left(2-5\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\)
\(d,\) Để \(A=-\dfrac{8}{5}\)
\(\Leftrightarrow\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}=-\dfrac{8}{5}\\ \Leftrightarrow10-25\sqrt{x}=-8\sqrt{x}-24\\ \Leftrightarrow17\sqrt{x}=34\\ \Leftrightarrow\sqrt{x}=2\\ \Leftrightarrow x=4\)
\(e,\) Để \(A=\sqrt{x}-\dfrac{18}{5}\)
\(\Leftrightarrow\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}=\sqrt{x}-\dfrac{18}{5}\\ \Leftrightarrow5\left(2-5\sqrt{x}\right)=5\sqrt{x}\left(\sqrt{x}+3\right)-18\left(\sqrt{x}+3\right)\\ \Leftrightarrow10-25\sqrt{x}=5x+15\sqrt{x}-18\sqrt{x}-54\\ \Leftrightarrow5x+22\sqrt{x}-64=0\\ \Leftrightarrow\left(\sqrt{x}-2\right)\left(32\sqrt{x}+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=-\dfrac{32}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x\in\varnothing\end{matrix}\right.\Leftrightarrow x=4\)
\(f,A< 0\Leftrightarrow\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}< 0\\ \Leftrightarrow2-5\sqrt{x}< 0\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow x>\dfrac{4}{25}\)
\(g,A>0\\ \Leftrightarrow\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}>0\\ \Leftrightarrow2-5\sqrt{x}>0\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow x< \dfrac{4}{25}\)
\(h,A>0\Leftrightarrow x< \dfrac{4}{25}\)
Mà \(x\in N\Leftrightarrow x=0\)
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
c: Ta có: \(A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}-\dfrac{3\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-5x+5\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)












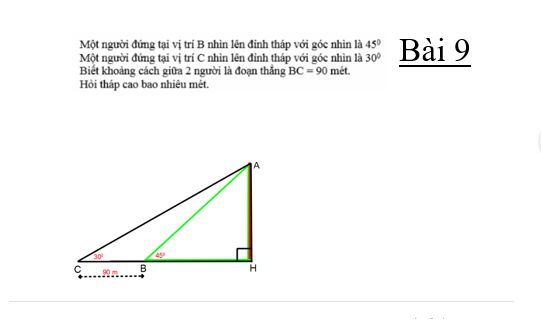 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ