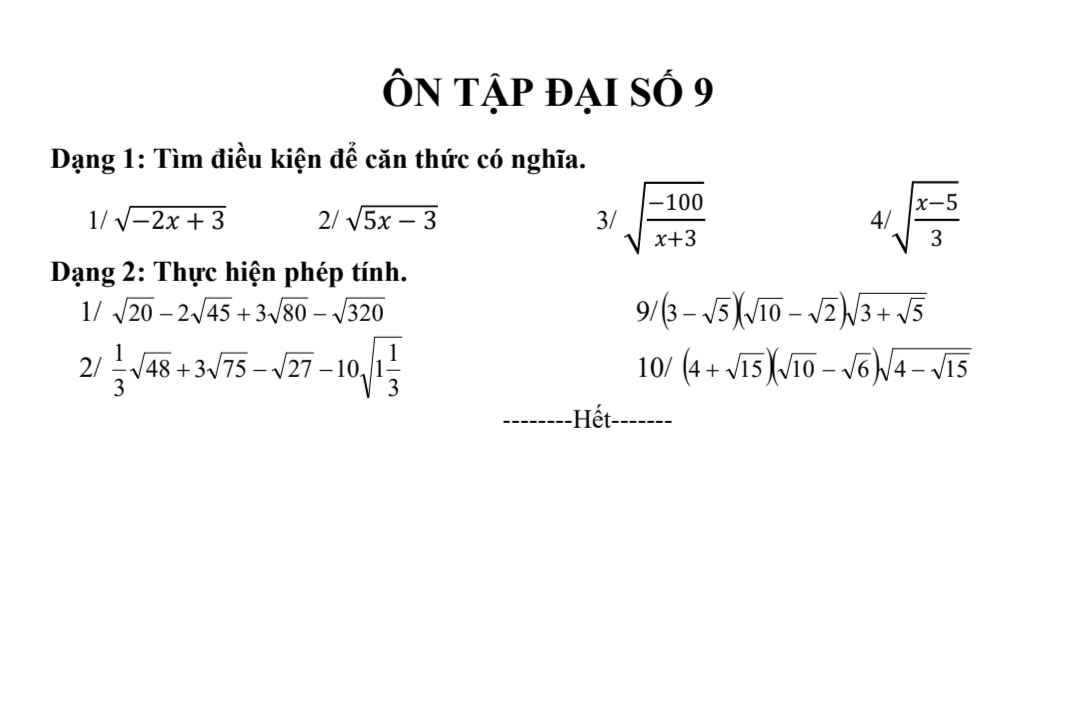
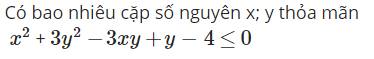Áp dụng BĐT:
\(\sqrt{x^2+a^2+u^2}+\sqrt{y^2+b^2+w^2}\ge\sqrt{\left(x+y\right)^2+\left(a+b\right)^2+\left(u+w\right)^2}\) (1)
Thật vậy (1)\(\Leftrightarrow x^2+a^2+u^2+y^2+b^2+w^2+2\sqrt{\left(x^2+a^2+u^2\right)\left(y^2+b^2+w^2\right)}\ge x^2+2xy+y^2+a^2+2ab+b^2+u^2+2uw+w^2\)
\(\Leftrightarrow\sqrt{x^2y^2+x^2b^2+x^2w^2+a^2y^2+a^2b^2+a^2w^2+u^2y^2+u^2b^2+u^2w^2}\ge xy+ab+uw\)
\(\Leftrightarrow x^2y^2+x^2b^2+x^2w^2+a^2y^2+a^2b^2+a^2w^2+u^2y^2+u^2b^2+u^2w^2\ge x^2y^2+a^2b^2+u^2w^2+2xyab+2abuw+2xyuw\)
\(\Leftrightarrow\left(x^2b^2-2xyab+a^2y^2\right)+\left(x^2w^2-2xyuw+u^2y^2\right)+\left(a^2w^2-2abuw+u^2b^2\right)\ge0\)
\(\Leftrightarrow\left(xb-ay\right)^2+\left(xw-uy\right)^2+\left(aw-ub\right)^2\ge0\) (lđ)
Dấu "=" xảy ra khi \(\dfrac{x}{y}=\dfrac{a}{b}=\dfrac{u}{w}\)
Áp dụng (1) vào A ta được:
\(A\ge\sqrt{\left(a+b\right)^2+\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\left(\dfrac{1}{b}+\dfrac{1}{c}\right)^2}+\sqrt{c^2+\dfrac{1}{c^2}+\dfrac{1}{a^2}}\)\(\ge\sqrt{\left(a+b+c\right)^2+\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2+\left(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{a}\right)^2}\)
\(\Leftrightarrow A\ge\sqrt{\left(a+b+c\right)^2+\left(\dfrac{9}{a+b+c}\right)^2+\left(\dfrac{9}{a+b+c}\right)^2}\)
\(\Leftrightarrow A\ge\dfrac{3\sqrt{33}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)
Vậy...











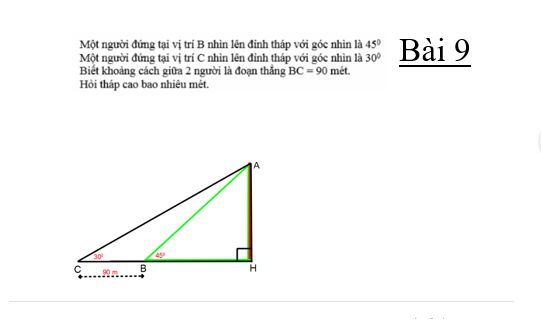 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ