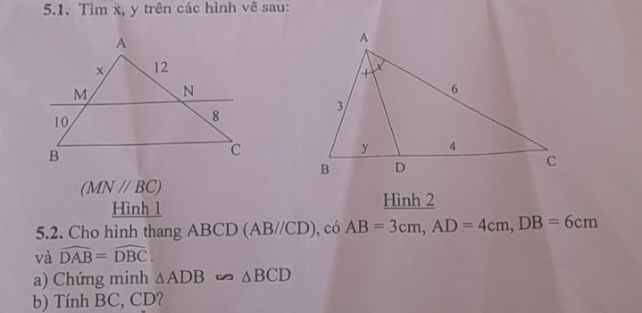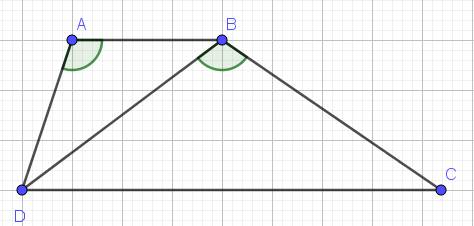
a) Sửa đề: Chứng minh \(\Delta DAB\) \(\sim\) \(\Delta CBD\)
Xét \(\Delta DAB\) và \(\Delta CBD\) có:
\(\widehat{DAB}=\widehat{CBD}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\) (so le trong)
\(\Rightarrow\Delta DAB\sim\Delta CBD\left(g-g\right)\)
b) Do \(\Delta DAB\sim\Delta CBD\) (cmt)
\(\Rightarrow\dfrac{AD}{BC}=\dfrac{AB}{BD}=\dfrac{BD}{CD}\)
*) \(\dfrac{AD}{BC}=\dfrac{AB}{BD}\)
\(\Rightarrow BC=\dfrac{AD.BD}{AB}\)
\(=\dfrac{4.6}{3}=8\left(cm\right)\)
*) \(\dfrac{AB}{BD}=\dfrac{BD}{CD}\)
\(\Rightarrow CD=\dfrac{BD.BD}{AB}\)
\(=\dfrac{6.6}{3}=12\left(cm\right)\)