42.
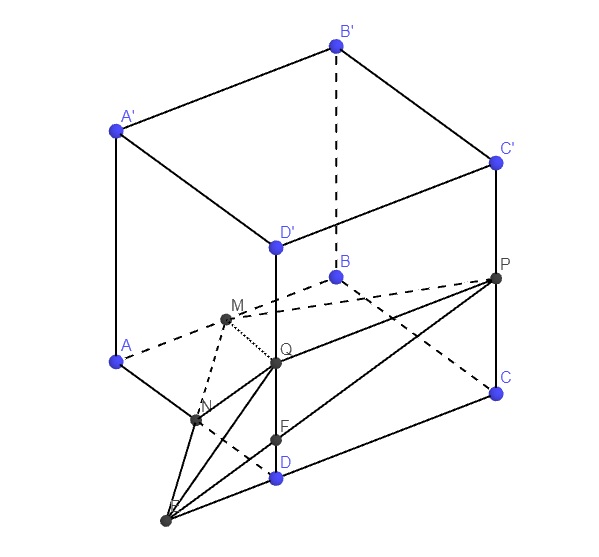
Do mọi hình hộp đều cho kết quả như nhau nên để đơn giản, chúng ta sẽ sử dụng hình hộp chữ nhật để tính toán (với 1 dạng hộp bất kì thì cần kẻ đường cao để tính tỉ lệ, như vậy rất mất thời gian, trong khi sử dụng hộp chữ nhật thì có thể sử dụng trực tiếp cạnh để tính, gọn hơn nhiều):
Nối MN kéo dài cắt CD tại E \(\Rightarrow AM=DE=\dfrac{1}{2}CD\)
Nối PE cắt D'D tại F \(\Rightarrow\dfrac{DF}{CP}=\dfrac{DE}{CE}=\dfrac{1}{3}\Rightarrow DF=\dfrac{1}{3}CP=\dfrac{1}{6}CC'\)
\(\Rightarrow QF=\dfrac{1}{2}CC'-\dfrac{1}{6}CC'=\dfrac{1}{3}CC'\)
\(V_{MNPQ}=V_{M.PQE}-\left(V_{E.NQF}+V_{P.NQF}\right)\)
Có:
\(V_{M.PQE}=\dfrac{1}{3}AD.\dfrac{1}{2}DQ.PQ=\dfrac{1}{12}AD.D'D.CD=\dfrac{1}{12}V\)
\(V_{E.NQF}=\dfrac{1}{3}.ED.\dfrac{1}{2}ND.QF=\dfrac{1}{3}.\dfrac{1}{2}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{72}V\)
\(V_{P.NQF}=\dfrac{1}{3}.PQ.\dfrac{1}{2}ND.QF=\dfrac{1}{3}CD.\dfrac{1}{2}.\dfrac{1}{2}AD.\dfrac{1}{3}D'D=\dfrac{1}{36}V\)
\(\Rightarrow V_{MNPQ}=\dfrac{1}{12}V-\left(\dfrac{1}{72}V+\dfrac{1}{36}V\right)=\dfrac{V}{24}\)
Bài này áp hệ trục tọa độ giải có lẽ sẽ ngắn hơn
43.
\(y'=2f'\left(2x+m\right)\) có cùng tính đơn điệu với hàm \(f\left(x\right)\)
Mà \(f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\) và \(\left(4;+\infty\right)\)
\(\Rightarrow y=f\left(2x+m\right)\) đồng biến trên các khoảng thỏa mãn:
\(\left[{}\begin{matrix}-1\le2x+m\le1\\2x+m\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{-1-m}{2}\le x\le\dfrac{1-m}{2}\\x\ge\dfrac{4-m}{2}\end{matrix}\right.\)
Hàm đồng biến trên \(\left(1;2\right)\) khi và chỉ khi:
\(\left[{}\begin{matrix}\dfrac{-1-m}{2}\le1< 2\le\dfrac{1-m}{2}\\1\ge\dfrac{4-m}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-3\\m\ge2\end{matrix}\right.\)
44.
\(y'=3x^2-6\left(m+2\right)x+3\left(m^2+4m\right)=3\left(x^2-2\left(m+2\right)x+m^2+4m\right)\)
\(=3\left(x^2-2mx+m^2-4x+4m\right)\)
\(=3\left[\left(x-m\right)^2-4\left(x-m\right)\right]\)
\(=3\left(x-m\right)\left(x-m-4\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(m;m+4\right)\)
Để hàm nghịch biến trên \(\left(0;1\right)\Rightarrow\left(0;1\right)\subset\left(m;m+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}m\le0\\m+4\ge1\end{matrix}\right.\) \(\Rightarrow-3\le m\le0\)
\(\Rightarrow\) Có 4 giá trị nguyên của m thỏa mãn
45.
Đường kính đáy nón là:
\(2R=\dfrac{2S}{h}=\dfrac{16.2}{4}=8\)
\(\Rightarrow R=4\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{64\pi}{3}\)
46.
Ko nhìn rõ đề, cái cơ số của \(\log_{...}\left(2018x+m\right)\) là cơ số mấy vậy nhỉ? 5 hay 6
47.
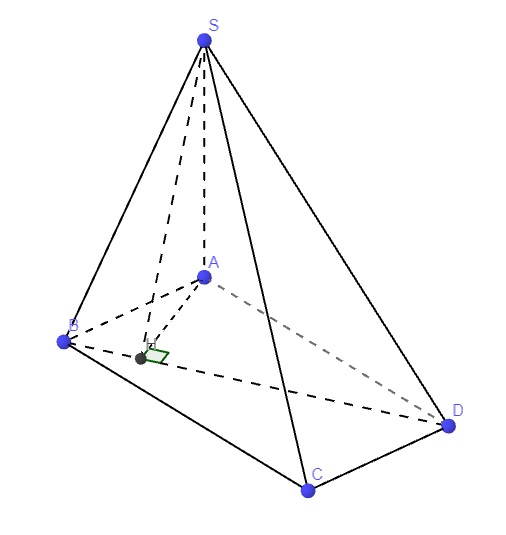
Trong mp (ABCD) từ A kẻ AH vuông góc BD
\(\Rightarrow\left\{{}\begin{matrix}BD\perp AH\\BD\perp SA\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAH\right)\)
\(\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\Rightarrow\widehat{SHA}=60^0\)
Áp dụng hệ thức lượng trong tam giác vuông ABD
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{3a}{\sqrt{10}}\)
\(\Rightarrow SA=AH.tan\widehat{SHA}=\dfrac{3a}{\sqrt{10}}.tan60^0=\dfrac{3a\sqrt{30}}{10}\)
\(V=\dfrac{1}{3}SA.AB.AD=\dfrac{3a^3\sqrt{30}}{10}\)