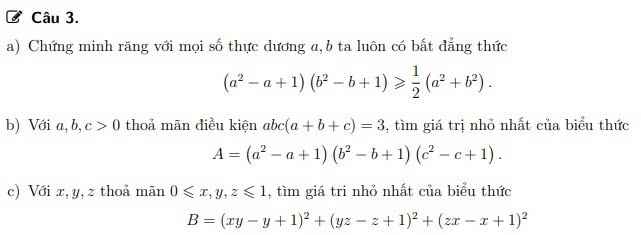Nhiều bài nhìn ngán quá, chỗ này ngắn nhất thì làm vậy:
a.
\(2\left(x^2-x+1\right)^2=\left(x^4+1\right)+\left(x-1\right)^4\ge x^4+1\)
\(\Rightarrow x^2-x+1\ge\sqrt{\dfrac{x^4+1}{2}}\)
\(\Rightarrow\left(a^2-a+1\right)\left(b^2-b+1\right)\ge\dfrac{\sqrt{\left(a^4+1\right)\left(1+b^4\right)}}{2}\ge\dfrac{\sqrt{\left(a^2+b^2\right)^2}}{2}=\dfrac{a^2+b^2}{2}\)
c.
Đặt \(\left\{{}\begin{matrix}a=y-xy=y\left(1-x\right)\\b=z\left(1-y\right)\\c=x\left(1-z\right)\end{matrix}\right.\)
Ta có:
\(xyz+\left(1-x\right)\left(1-y\right)\left(1-z\right)\ge0\)
\(\Leftrightarrow1+xy+yz+zx-x-y-z\ge0\)
\(\Rightarrow x+y+z-xy-yz-zx\le1\)
Do đó:
\(ab+bc+ca=xy\left(1-x\right)\left(1-z\right)+yz\left(1-x\right)\left(1-y\right)+zx\left(1-y\right)\left(1-z\right)\)
\(\le\dfrac{1}{4}y\left(1-z\right)\left(x+1-x\right)+\dfrac{1}{4}z\left(1-x\right)\left(y+1-y\right)+\dfrac{1}{4}x\left(1-y\right)\left(z+1-z\right)\)
\(=\dfrac{1}{4}y\left(1-z\right)+\dfrac{1}{4}z\left(1-x\right)+\dfrac{1}{4}x\left(1-y\right)\)
\(=\dfrac{1}{4}\left(x+y+z-xy-yz-zx\right)\le\dfrac{1}{4}\)
\(\Rightarrow\dfrac{1}{2}\ge2\left(ab+bc+ca\right)\)
\(B=\left(1-a\right)^2+\left(1-b\right)^2+\left(1-c\right)^2\)
\(=3+a^2+b^2+c^2-2a-2b-2c\)
\(=\dfrac{5}{2}+\dfrac{1}{2}+a^2+b^2+c^2-2\left(a+b+c\right)\)
\(\ge\dfrac{5}{2}+2\left(ab+bc+ca\right)+a^2+b^2+c^2-2\left(a+b+c\right)\)
\(=\dfrac{3}{2}+\left(a+b+c-1\right)^2\ge\dfrac{3}{2}\)
b.
\(a^2b^2+b^2c^2+c^2a^2\ge abc\left(a+b+c\right)=3\)
Áp dụng BĐT chứng minh ở câu a:
\(A^2\ge\dfrac{\left(a^4+1\right)\left(b^4+1\right)\left(c^4+1\right)}{8}=\dfrac{\left(2a^4+2\right)\left(b^4c^4+b^4+c^4+1\right)}{16}\)
\(=\dfrac{\left(1+a^4+a^4+1\right)\left(b^4c^4+b^4+c^4+1\right)}{16}\)
\(\ge\dfrac{\left(b^2c^2+a^2b^2+a^2c^2+1\right)^2}{16}\ge\dfrac{\left(3+1\right)^2}{16}=1\)
\(\Rightarrow A\ge1\)