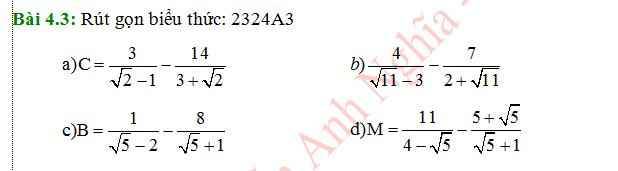a)
\(C=\dfrac{3}{\sqrt{2}-1}-\dfrac{14}{3+\sqrt{2}}\\ =\dfrac{3\left(\sqrt{2}+1\right)}{2-1}-\dfrac{14\left(3-\sqrt{2}\right)}{9-2}\\ =3\sqrt{2}+3-\dfrac{14\left(3-\sqrt{2}\right)}{7}\\ =3\sqrt{2}+3-2\left(3-\sqrt{2}\right)\\ =3\sqrt{2}+3-6+2\sqrt{2}\\ =5\sqrt{2}-3\)
b)
\(\dfrac{4}{\sqrt{11}-3}-\dfrac{7}{2+\sqrt{11}}\\ =\dfrac{4\left(\sqrt{11}+3\right)}{11-9}-\dfrac{7\left(2-\sqrt{11}\right)}{4-11}\\ =\dfrac{4\left(\sqrt{11}+3\right)}{2}-\dfrac{7\left(2-\sqrt{11}\right)}{-7}\\ =2\left(\sqrt{11}+3\right)+2-\sqrt{11}\\ =2\sqrt{11}+6+2-\sqrt{11}\\ =\sqrt{11}+8\)
c)
\(B=\dfrac{1}{\sqrt{5}-2}-\dfrac{8}{\sqrt{5}+1}\\ =\dfrac{\sqrt{5}+2}{5-4}-\dfrac{8\left(\sqrt{5}-1\right)}{5-1}\\ =\sqrt{5}+2-\dfrac{8\left(\sqrt{5}-1\right)}{4}\\ =\sqrt{5}+2-2\left(\sqrt{5}-1\right)\\ =\sqrt{5}+2-2\sqrt{5}+2\\ =-\sqrt{5}+4\)
d)
\(M=\dfrac{11}{4-\sqrt{5}}-\dfrac{5+\sqrt{5}}{\sqrt{5}+1}\\ =\dfrac{11\left(4+\sqrt{5}\right)}{16-5}-\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\\ =\dfrac{11\left(4+\sqrt{5}\right)}{11}-\sqrt{5}\\ =4+\sqrt{5}-\sqrt{5}\\ =4\)