a)
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\\sqrt{x}-1\ne0\\\sqrt{x}+2\ne0\forall x\\2\sqrt{x}+1\ne0\forall x\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\\sqrt{x}\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
\(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\\ \Leftrightarrow P=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\\ \Leftrightarrow P=\dfrac{\left(2\sqrt{x}+1\right).\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)\left(2\sqrt{x}+1\right)}\\ \Leftrightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
b)
\(P=\dfrac{3}{5}\Rightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{3}{5}\\ \Leftrightarrow5\sqrt{x}=3\left(\sqrt{x}+2\right)\\ \Leftrightarrow5\sqrt{x}=3\sqrt{x}+6\\ \Leftrightarrow2\sqrt{x}=6\\ \Leftrightarrow\sqrt{x}=3\\ \Leftrightarrow x=9\left(tm\right)\)
Vậy x = 9

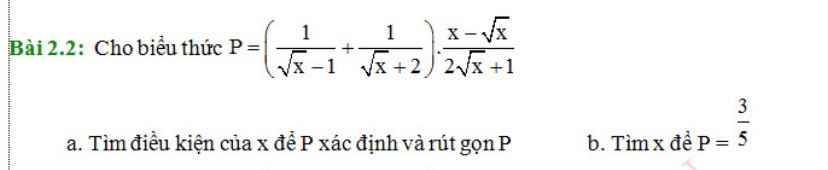



















 giúp e vs ạ :<
giúp e vs ạ :<