\(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x-2\sqrt{x}+1}\left(\text{đ}k\text{x}\text{đ}:x\ge0;x\ne1\right)\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x-2\sqrt{x}+1}{\sqrt{x}+1}\\ =\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\dfrac{x-2\sqrt{x}+1}{\sqrt{x}+1}\\ =\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
__
Ta có :
\(\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\\ \Leftrightarrow\dfrac{3\left(\sqrt{x}-1\right)}{3\sqrt{x}}=\dfrac{\sqrt{x}}{3\sqrt{x}}\\ \Leftrightarrow3\sqrt{x}-3=\sqrt{x}\\ \Leftrightarrow2\sqrt{x}=3\\ \Leftrightarrow\sqrt{x}=\dfrac{3}{2}\\ \Leftrightarrow x=\dfrac{9}{4}\)

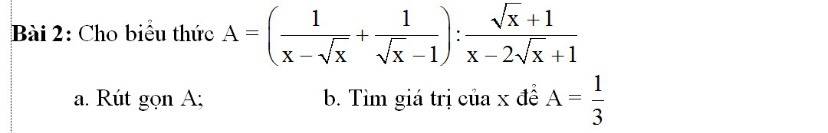



















 giúp e vs ạ :<
giúp e vs ạ :<