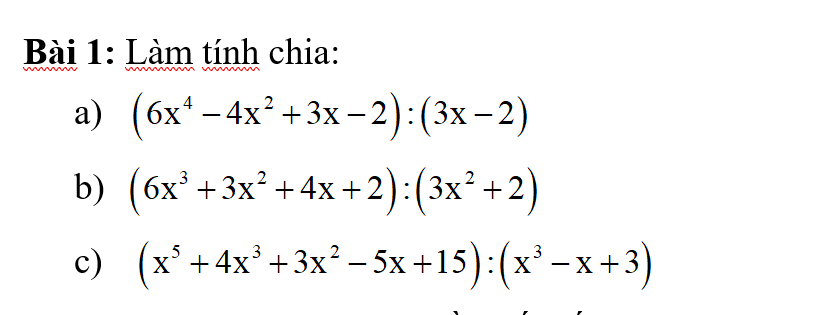\(A=x^3+y^3+z^3-3xyz\\=(x+y)^3+z^3-3xy(x+y)-3xyz\\=(x+y+z)^3-3(x+y)z(x+y+z)-3xy(x+y+z)\\=(x+y+z)[(x+y+z)^2-3(x+y)z-3xy]\\=(x+y+z)(x^2+y^2+z^2+2xy+2yz+2xz-3xz-3yz-3xy)\\=(x+y+z)(x^2+y^2+z^2-xy-yz-xz)\)
Các HĐT được sử dụng:
\(a^3+b^3=(a+b)^3-3ab(a+b)\\(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac\)
Đúng 2
Bình luận (0)
huhu giúp e với ạ e cần gấp ạ
