Question

giúp e nha

Answer 1

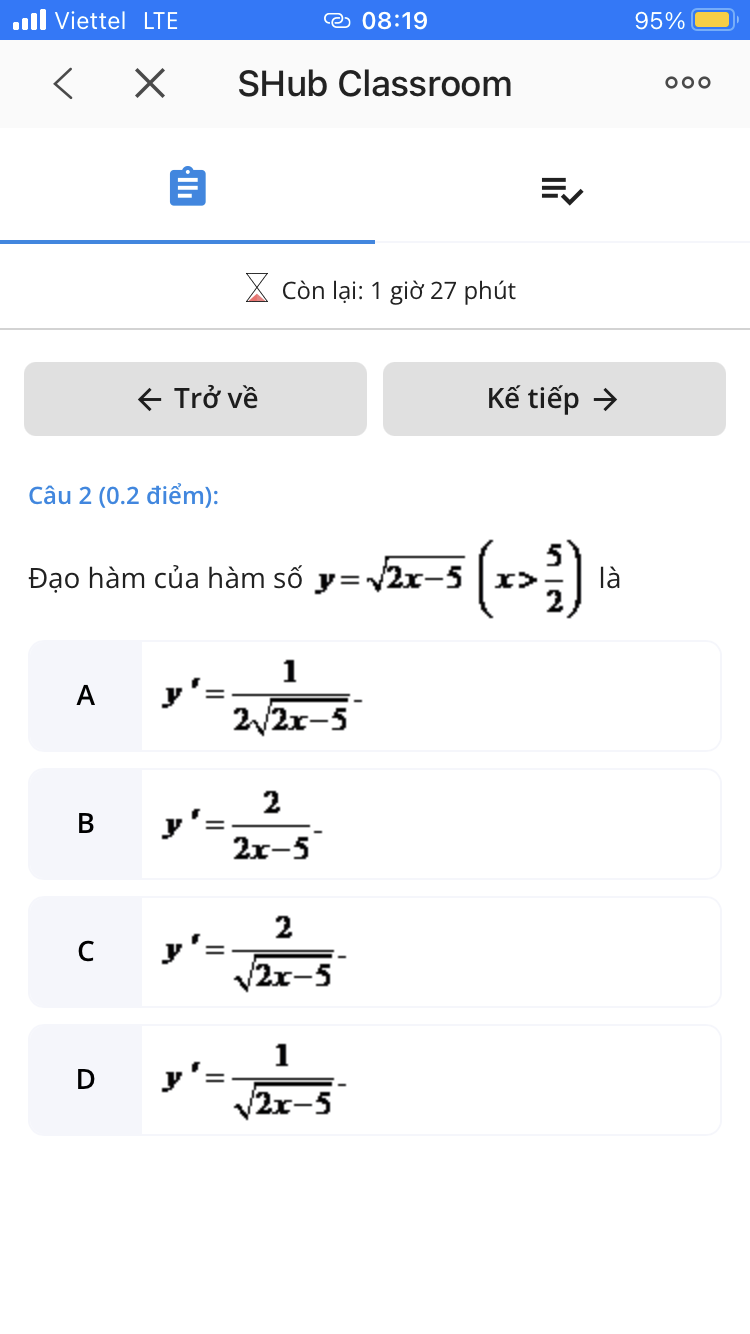
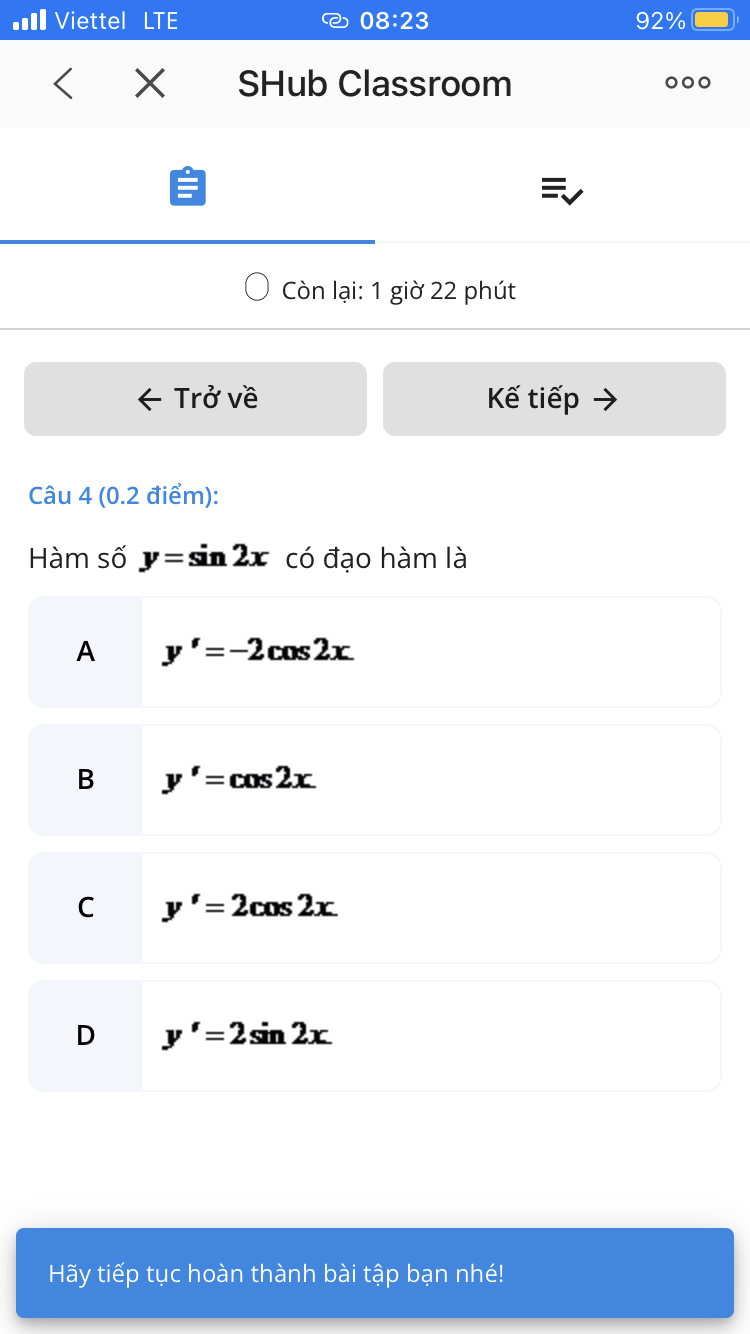
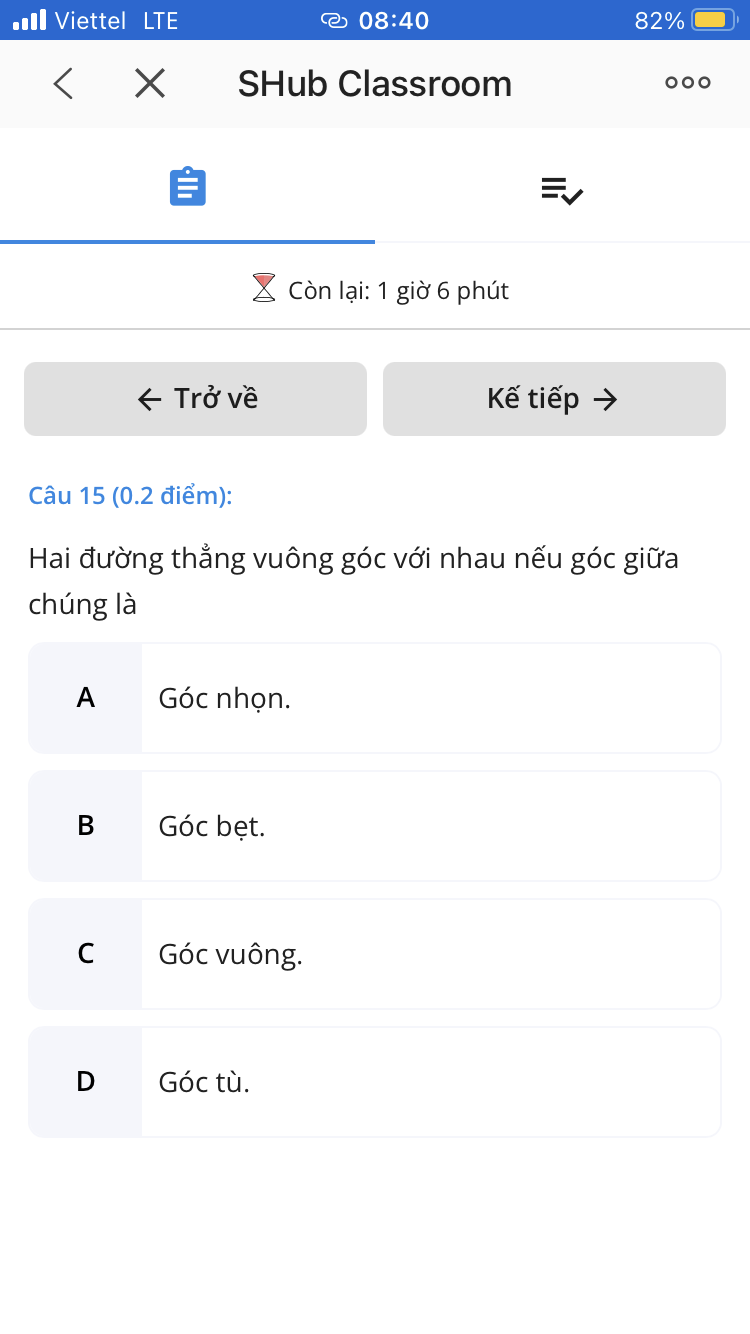
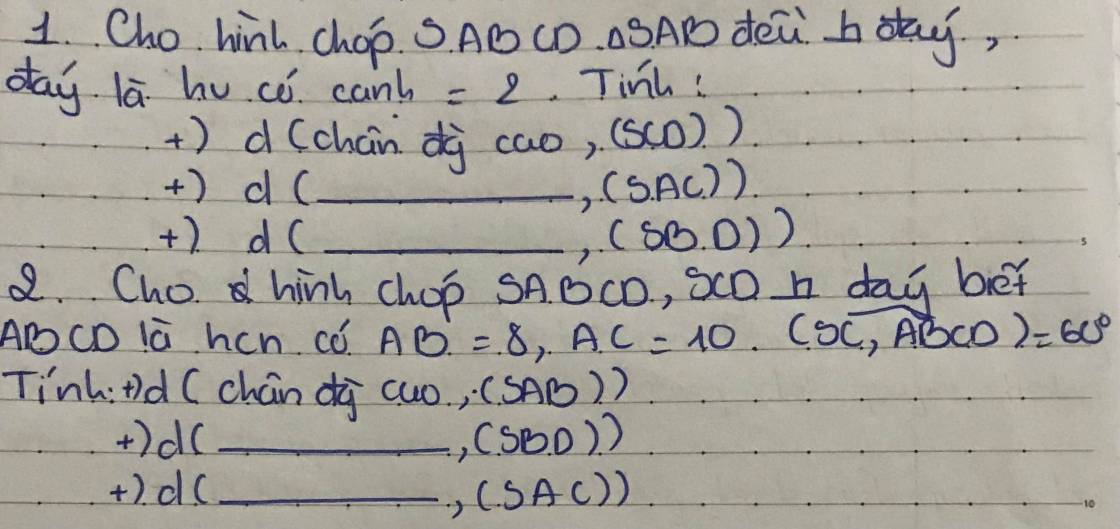Câu 2:

\(\lim_{t\to5^{-}}v\left(t\right)=\lim_{t\to5^{-}}10+a=10+a\)

\(v\left(5\right)=10+a\)

\(\lim_{t\to5^{+}}v\left(t\right)=\lim_{t\to5^{+}}5^2-5\cdot5+10=10\)

Để v(t) liên tục khi t=5 thì 10+a=10

=>a=0

Câu 1:, \(\lim_{x\to1^{+}}f\left(x\right)=\lim_{x\to1^{+}}x^2-3x-4=1^2-3\cdot1-4=1-3-4=-6\)

\(f\left(1\right)=1^2-3\cdot1-4=1-3-4=-2-4=-6\)

\(\lim_{x\to1^{-}}f\left(x\right)=\lim_{x\to1^{-}}m=m\)

Để hàm số liên tục tại x=1 thì m=-6