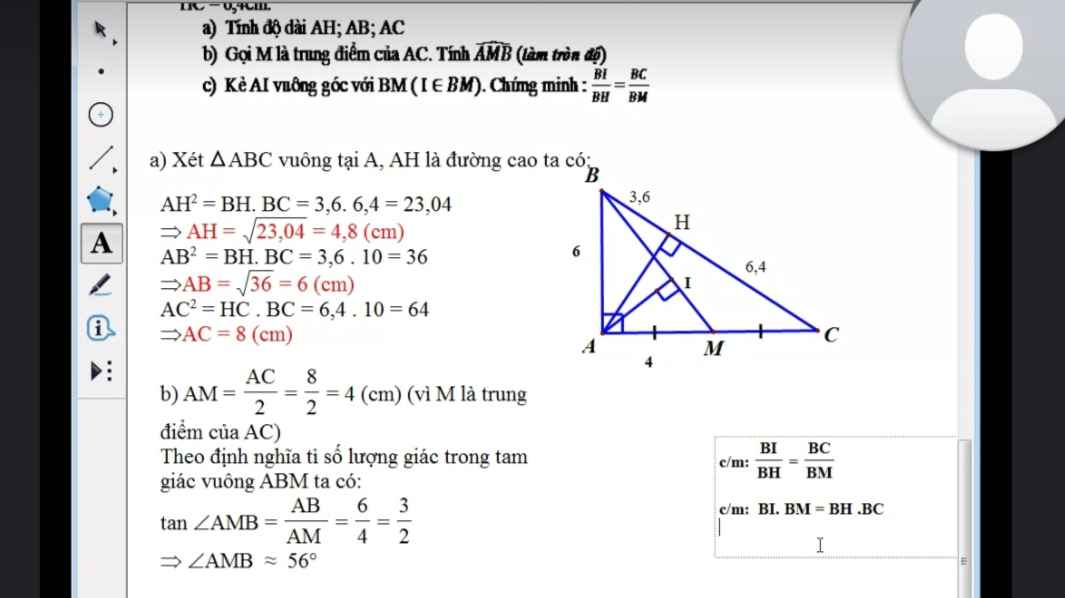
c, Áp dụng HTL ta được \(\left\{{}\begin{matrix}BI\cdot BM=AB^2\\BH\cdot BC=AB^2\end{matrix}\right.\Rightarrow BI\cdot BM=BH\cdot BC\)
\(\Rightarrow\dfrac{BI}{BH}=\dfrac{BC}{BM}\)
c: Xét ΔABM vuông tại A có AI là đường cao
nên \(BI\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BI\cdot BM=BH\cdot BC\)
hay \(\dfrac{BI}{BH}=\dfrac{BC}{BM}\)












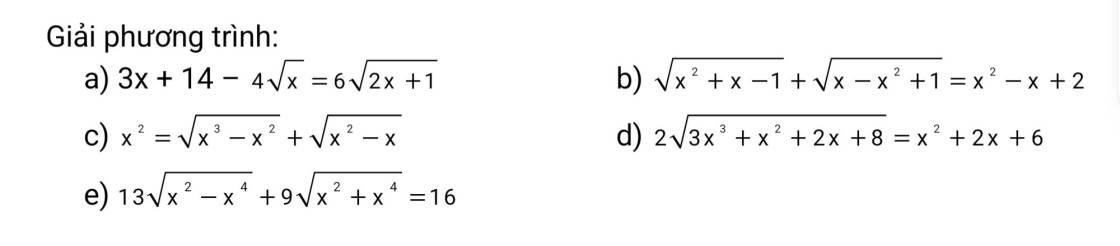 Nhờ mn giúp câu c , e ạ .
Nhờ mn giúp câu c , e ạ . 




 không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn


