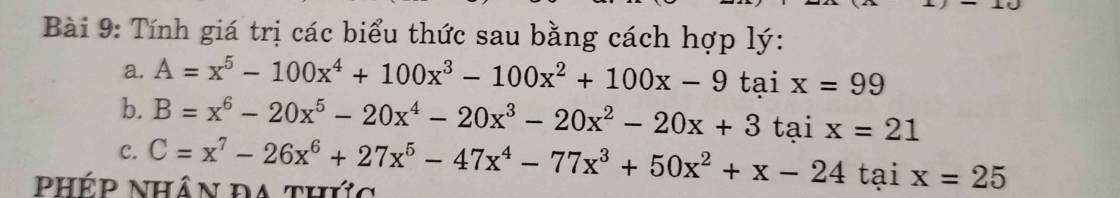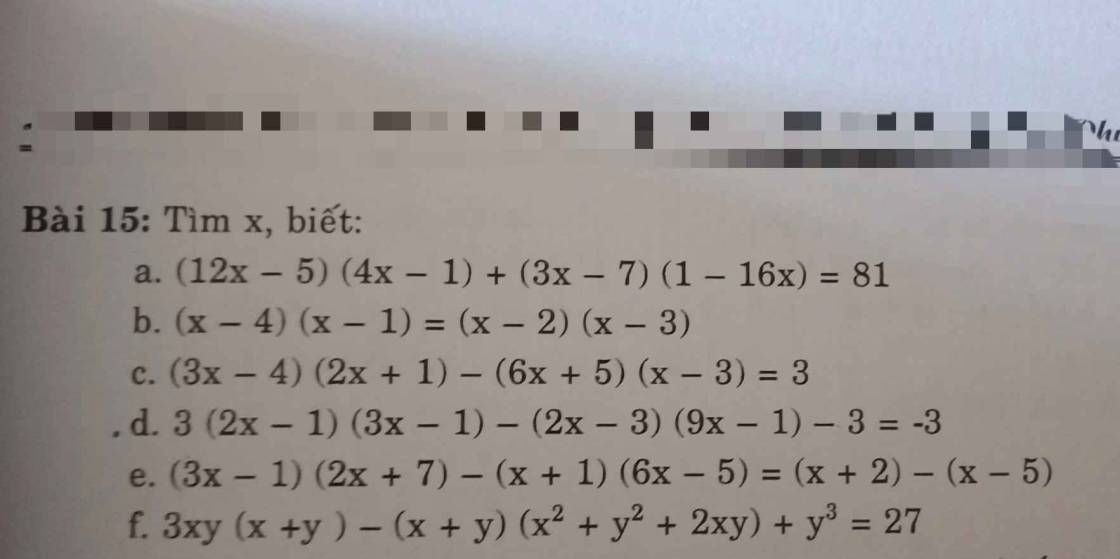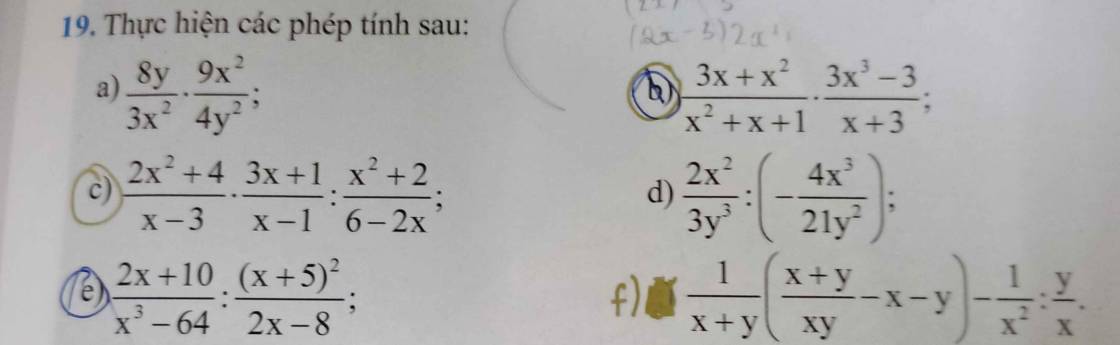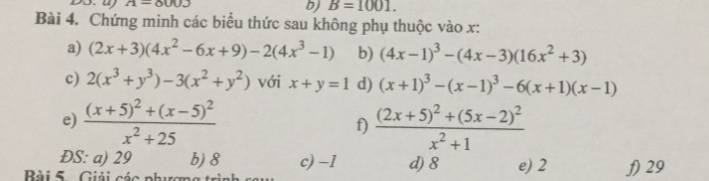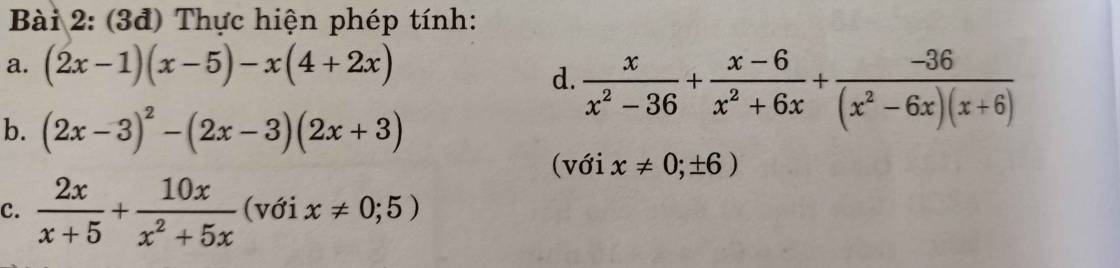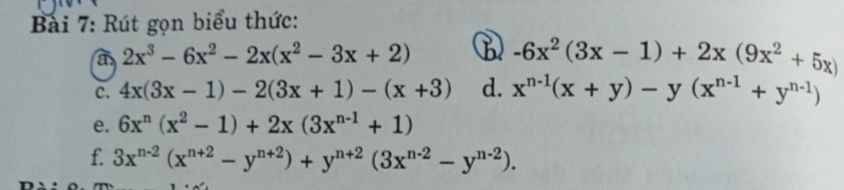Bài 4:
a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\hat{HAB}=\hat{HCA}\left(=90^0-\hat{HBA}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\frac{HA}{HC}=\frac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
b: Xét ΔDAC vuông tại A và ΔDKB vuông tại K có
\(\hat{ADC}=\hat{KDB}\) (hai góc đối đỉnh)
Do đó: ΔDAC~ΔDKB
=>\(\hat{DCA}=\hat{DBK}\)
mà \(\hat{DCA}=\hat{DCB}\) (CD là phân giác của góc ACB)
nên \(\hat{KBD}=\hat{KCB}\)
Xét ΔKBD vuông tại K và ΔKCB vuông tại K có
\(\hat{KBD}=\hat{KCB}\)
Do đó: ΔKBD~ΔKCB
=>\(\frac{KD}{KB}=\frac{BD}{CB}\) (1)
Xét ΔCAB có CD là phân giác
nên \(\frac{DA}{DB}=\frac{CA}{CB}\)
=>\(\frac{DA}{AC}=\frac{DB}{CB}\left(2\right)\)
Xét ΔCAD vuông tại A và ΔCHI vuông tại H có
\(\hat{ACD}=\hat{HCI}\) (CD là phân giác của góc ACB)
Do đó: ΔCAD~ΔCHI
=>\(\frac{AC}{HC}=\frac{AD}{HI}\)
=>\(\frac{AD}{AC}=\frac{HI}{HC}\) (3)
Từ (1),(2),(3) suy ra \(\frac{HI}{HC}=\frac{KB}{KD}\)
=>\(HI\cdot KD=HC\cdot KB\)
c: Xét ΔBHE vuông tại H và ΔBKC vuông tại K có
\(\hat{HBE}\) chung
Do đó: ΔBHE~ΔBKC
=>\(\frac{BH}{BK}=\frac{BE}{BC}\)
=>\(BE\cdot BK=BH\cdot BC\left(4\right)\)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\hat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\frac{BH}{BA}=\frac{BA}{BC}\)
=>\(BH\cdot BC=BA^2\)
mà BA=BF
nên \(BH\cdot BC=BF^2\left(5\right)\)
Từ (3),(4) suy ra \(BF^2=BK\cdot BE\)
=>\(\frac{BF}{BK}=\frac{BE}{BF}\)
Xét ΔBFE và ΔBKF có
\(\frac{BF}{BK}=\frac{BE}{BF}\)
góc FBE chung
Do đó: ΔBFE~ΔBKF
=>\(\hat{BFE}=\hat{BKF}=90^0\)
=>FE⊥FB tại F