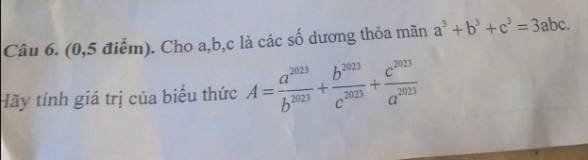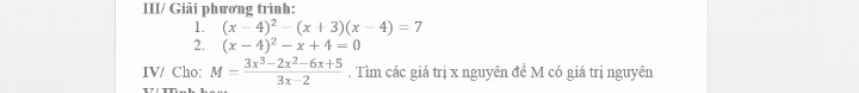Question

Giúp ạ đang giải đề cương

Answer 1

a.Xét tam giác AHB và tam giác CHA, có:

\(\widehat{AHB}=\widehat{CHA}=90^o\)

\(\widehat{HAB}=\widehat{HCA}\) ( cùng phụ \(\widehat{HAC}\)) 

Vậy tam giác AHB đồng dạng tam giác CHA ( g.g )

b.Áp dụng định lý pitago trong tam giác vuông ABC:

\(BC=\sqrt{6^2+8^2}=\sqrt{100}=10\left(cm\right)\)

Xét tam giác AHB và tam giác CAB, có:

\(\widehat{B}\): chung

\(\widehat{AHB}=\widehat{CAB}=90^o\)

Vậy tam giác AHB đồng dạng tam giác CAB ( g.g )

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\)

\(\Leftrightarrow\dfrac{6}{10}=\dfrac{HB}{6}\)

\(\Leftrightarrow HB=\dfrac{6.6}{10}=3,6\left(cm\right)\)