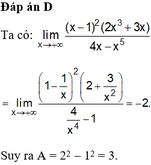Các câu hỏi tương tự
Giới hạn
lim
x
→
3
x
+
1
-
5
x
+
1
x
-
4
x
-
3...
Đọc tiếp
Giới hạn lim x → 3 x + 1 - 5 x + 1 x - 4 x - 3 bằng a b (phân số tối giản). Giá trị của a - b là:
A. 1
B. 1 9
C. -1
D. 2
Giới hạn
lim
x
→
2
x
+
1
-
5
x
-
1
2
-
3
x
-
2
bằng
a
b
(phân số tối giả...
Đọc tiếp
Giới hạn lim x → 2 x + 1 - 5 x - 1 2 - 3 x - 2 bằng a b (phân số tối giản). Giá trị của A = |2a/b + a/2| là:
A. 2 9
B. - 2 9
C. - 5 9
D. 13 9
Giới hạn
lim
x
→
1
4
x
6
-
5
x
2
+
x
x
2
-
1
bằng
a
b
(phân số tối giản). Giá trị...
Đọc tiếp
Giới hạn lim x → 1 4 x 6 - 5 x 2 + x x 2 - 1 bằng a b (phân số tối giản). Giá trị của A = |a| - 5|b| là:
A. 15
B. 10
C. 5
D. 0
Cho hàm số
y
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tập tất cả các giá trị của m để đồ thị hàm số
y
f
x
có 5 điểm cực trị là...
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Biết rằng
9
x
+
9
−
x
23.
Khi đó biểu thức
A
5
+
3
x
+
3
−
x
1
−
3...
Đọc tiếp
Biết rằng 9 x + 9 − x = 23. Khi đó biểu thức A = 5 + 3 x + 3 − x 1 − 3 x − 3 − x = a b với a b là phân số tối giản và a , b ∈ ℤ . Tích a.b có giá trị bằng
A. 10
B. 8
C. -8
D. -10
Giới hạn
l
i
m
x
→
3
x
+
1
-
5
x
+
1
x
-
4
x
-
3...
Đọc tiếp
Giới hạn l i m x → 3 x + 1 - 5 x + 1 x - 4 x - 3 bằng a b (phân số tối giản). Giá trị của a - b là:
A. 1
B. 1 9
C. -1
D. 9 8
Gọi a, b là hai giá trị thực để hàm số
f
x
2
x
2
+
6
3
−
a...
Đọc tiếp
Gọi a, b là hai giá trị thực để hàm số f x = 2 x 2 + 6 3 − a x x 2 − 1 , x ≠ 1 a + b x + 2 , x = 1 liên tục tại x = 1. Biết rằng b = m n ; m ∈ ℤ , n ∈ ℕ và m n là phân số tối giản. Tính P = m + 2n
A. P = -17
B. P = =-5
C. P = -23
D. P = -13
Giới hạn
l
i
m
x
→
0
x
+
9
+
x
+
16
-
7
x
bằng
a
b
(phân số tối giản) thì giá t...
Đọc tiếp
Giới hạn l i m x → 0 x + 9 + x + 16 - 7 x bằng a b (phân số tối giản) thì giá trị A = b a - b 8 là:
A. 7 24
B. 3 7
C. 22 7
D. 7 22
Cho hàm số
f
x
3
x
−
4
+
x
+
1
.2
7
−
x
−
6
x
+
3
. Giả sử
m
0
a
b
(...
Đọc tiếp
Cho hàm số f x = 3 x − 4 + x + 1 .2 7 − x − 6 x + 3 . Giả sử m 0 = a b ( a , b ∈ ℤ , a b là phân số tối giản) là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 − 4 6 x − 9 x 2 + 2 m − 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. P = -1
B. P = 7
C. P = 11
D. P = 9