Các câu hỏi tương tự
Tính giới hạn sau:
1) \(\lim\limits_{n\rightarrow\infty}\dfrac{1}{n^3}\left(1+2^2+...+\left(n-1\right)^2\right)\)
2) \(\lim\limits_{n\rightarrow\infty}\dfrac{1}{n}[\left(x+\dfrac{a}{n}\right)+\left(x+\dfrac{2a}{n}\right)+...+\left(x+\dfrac{\left(n-1\right)a}{n}\right)]\)
3) \(\lim\limits_{n\rightarrow\infty}\dfrac{1^3+2^3+...+n^3}{n^4}\)
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳn...
Đọc tiếp
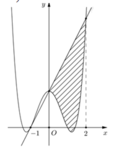
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho dãy un xác định bởi \(u_1=1\)và \(\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\).Chứng minh dãy đó có giới hạn và tìm giới hạn dãy đó
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
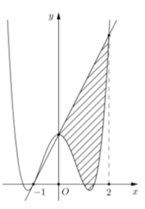
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Tìm giới hạn(Không dùng máy tính)
`lim(3-2x)/(sqrtx-3)`
Kết quả `=-oo` nhưng mình không biết làm thế nào. ;-;
Xét hàm số y f(x) liên tục trên miền D [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x a; x b Người ta chứng minh được rằng độ dài đường cong S bằng
∫
a
b
1
+
(
f
(
x
)
)
2
d
x
...
Đọc tiếp
Xét hàm số y = f(x) liên tục trên miền D = [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x = a; x = b Người ta chứng minh được rằng độ dài đường cong S bằng ∫ a b 1 + ( f ' ( x ) ) 2 d x Theo kết quả trên, độ dài đường cong S là phần đồ thị của hàm số f(x) = ln x và bị giới hạn bởi các đường thẳng x = 1 ; x = 3 là m - m + ln 1 + m n với m , n ∈ R thì giá trị của m 2 - m n + n 2 là bao nhiêu?
A. 6
B. 7
C. 3
D. 1
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π/2 bằng:
A. 1; B. 2/7;
C. 2π; D. 2π/3.
Diện tích hình phẳng P giới hạn bởi các đường: y 1 = x, y 2 = 2x, y 3 = 2 - x bằng:
A. 1 B. 2/3
C. 2 D. 1/3