Chọn B.
Tọa độ giao điểm là nghiệm của hệ phương trình:
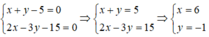
Chọn B.
Tọa độ giao điểm là nghiệm của hệ phương trình:
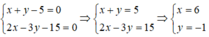
Giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y + 5 = 0 có tọa độ là
A. (2;3)
B. (1;1)
C. (-2;-3)
D. (4;1)
Tìm tọa độ giao điểm của đường thẳng ( a) : 4x- y-5= 0 và đường thẳng (b) : 2x- 3y – 5= 0.
A. (1; 1)
B. Không có giao điểm.
C. (1; -1)
D. Có vô số điểm chung
Tìm tọa độ giao điểm của đường thẳng (d) : 2x- 3y+ 12= 0 và đường thẳng y= 2
A. (2; 2)
B. (-3; 2)
C. (3; 2)
D. ( 2; 3)
Tọa độ giao điểm của hai đường thẳng d: x - 3y - 1 = 0; d ' = x = 2 t y = 3 - t là:
A. (1;4)
B. (-1;4)
C. (4;1)
D. (4;-1)
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có AB :2x -y + 1 = 0, AC : x -y + 1 = 0 và M là trung điểm của CD thuộc đường thẳng 2x + y + 1 = 0 . Tìm tọa độ các đỉnh A, B, C, D
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
Cho 2 điểm P(1;6) và Q(-3;-4) và đường thẳng △: 2x - y - 1 = 0. Tọa độ điểm M thuộc △ sao cho MP + MQ nhỏ nhất.
A. M(0;-1)
B. M(2;3)
C. M(1;1)
D. M(3;5)
Tam giác ABC biết A (2;-1) và phương trình hai đường phân giác trong của góc B và góc C lần lượt là d: x - 2y + 1=0, d2 : 2x - 3y + 6 = 0 . Xác định tọa độ B, C.