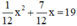
⇔ x2 + 7x = 228
⇔ x2 + 7x – 228 = 0
Có a = 1; b = 7; c = -228; Δ = b2 – 4ac = 72 – 4.1.(-228) = 961 > 0
Phương trình có hai nghiệm:
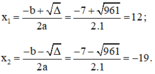
Vậy phương trình có hai nghiệm x1 = 12 và x2 = -19.
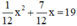
⇔ x2 + 7x = 228
⇔ x2 + 7x – 228 = 0
Có a = 1; b = 7; c = -228; Δ = b2 – 4ac = 72 – 4.1.(-228) = 961 > 0
Phương trình có hai nghiệm:
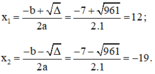
Vậy phương trình có hai nghiệm x1 = 12 và x2 = -19.
Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):
a ) x 2 = 12 x + 288 b ) 1 12 x 2 + 7 12 x = 19
Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):
x 2 = 12 x + 288
Giải hẹ phương trình:
\(\dfrac{12}{x-1}+\dfrac{7}{y+3}=19\)
\(\dfrac{2x+6}{x-1}+\dfrac{3y+14}{y+3}=18\)
\(2x-x^2-\sqrt{6x^2-12+7}=0\)
Giải phương trình
giải phương trình
\(\left(x+1\right)\sqrt{x+2}+\left(x+6\right)\sqrt{x+7}=x^2+7x+12\)
7. Phương trình bậc hai.
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠0)

Giải phương trình vô tỉ :
a) \(\sqrt{7x^2+25x+19}-\sqrt{x^2-2x-25}=7\sqrt{x+2}\)
b) \(\sqrt{4x^2+24x+35}-\sqrt{x^2+3x+2}=\sqrt{x^2+7x+12}\)
Giải bất phương trình sau: \(\dfrac{x^2-26}{10}\)+\(\dfrac{x^2-25}{11}\) \(\ge\) \(\dfrac{x^2-24}{12}\)+\(\dfrac{x^2-23}{13}\)
giải hệ phương trình\(\hept{\begin{cases}x+y=-6\\\sqrt{\frac{y+2}{2x-1}}+\sqrt{\frac{2x-1}{y+2}}=2\end{cases}}\)
giải phương trình \(\frac{6}{x^2-9}+\frac{4}{x^2-11}-\frac{7}{x^2-8}-\frac{3}{x^2-12}=0\)