Bài 10: Ta có: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
=>\(\sqrt{p\cdot\left(p-a\right)\left(p-b\right)\left(p-c\right)}=p\left(p-a\right)\)
=>\(p\left(p-a\right)\left(p-b\right)\left(p-c\right)=p^2\cdot\left(p-a\right)^2\)
=>\(\left(p-b\right)\left(p-c\right)=p\left(p-a\right)\) (Vì p(p-a)>0)
=>\(\left(\frac{a+b+c}{2}-b\right)\left(\frac{a+b+c}{2}-c\right)=\frac{a+b+c}{2}\left(\frac{a+b+c}{2}-a\right)\)
=>\(\frac{a-b+c}{2}\cdot\frac{a+b-c}{2}=\frac{a+b+c}{2}\cdot\frac{b+c-a}{2}\)
=>(a-b+c)(a+b-c)=(a+b+c)(-a+b+c)
=>\(a^2-\left(b-c\right)^2=\left(b+c\right)^2-a^2\)
=>\(a^2+a^2=\left(b+c\right)^2+\left(b-c\right)^2\)
=>\(2a^2=b^2+2bc+c^2+b^2-2bc+c^2=2b^2+2c^2\)
=>\(a^2=b^2+c^2\)
=>ΔABC vuông tại A
Bài 6:
a: Xét ΔABC có \(cosA=\frac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\frac{8^2+12^2-16^2}{2\cdot8\cdot12}\)
\(=\frac{64+144-256}{16\cdot12}=\frac{-48}{16\cdot12}=\frac{-3}{12}=-\frac14\)
=>\(\hat{A}\) ≃104 độ 28p
Xét ΔABC có \(cosB=\frac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\frac{8^2+16^2-12^2}{2\cdot8\cdot16}=\frac{176}{16\cdot16}=\frac{11}{16}\)
=>\(\hat{B}\) ≃46 độ 34p
Xét ΔABC có \(\hat{A}+\hat{B}+\hat{C}=180^0\)
=>\(\hat{C}=180^0-104^028^{\prime}-46^034^{\prime}=28^058^{\prime}\)
b: \(\sin^2A+cos^2A=1\)
=>\(\sin^2A=1-\left(-\frac14\right)^2=1-\frac{1}{16}=\frac{15}{16}\)
=>\(\sin A=\sqrt{\frac{15}{16}}=\frac{\sqrt{15}}{4}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AB\cdot AC\cdot\sin A\)
\(=\frac12\cdot8\cdot12\cdot\frac{\sqrt{15}}{4}=6\cdot2\sqrt{15}=12\sqrt{15}\left(\operatorname{cm}^2\right)\)
Độ dài đường cao kẻ từ B là:
\(h_{B}=\frac{2\cdot S_{ABC}}{AC}=\frac{2\cdot12\sqrt{15}}{12}=2\sqrt{15}\left(\operatorname{cm}\right)\)
c:Xét ΔABC có AM là đường trung tuyến
nên \(AM^2=\frac{AB^2+AC^2}{2}-\frac{BC^2}{4}=\frac{8^2+12^2}{2}-\frac{16^2}{4}=40\)
=>\(AM=\sqrt{40}=2\sqrt{10}\left(\operatorname{cm}\right)\)













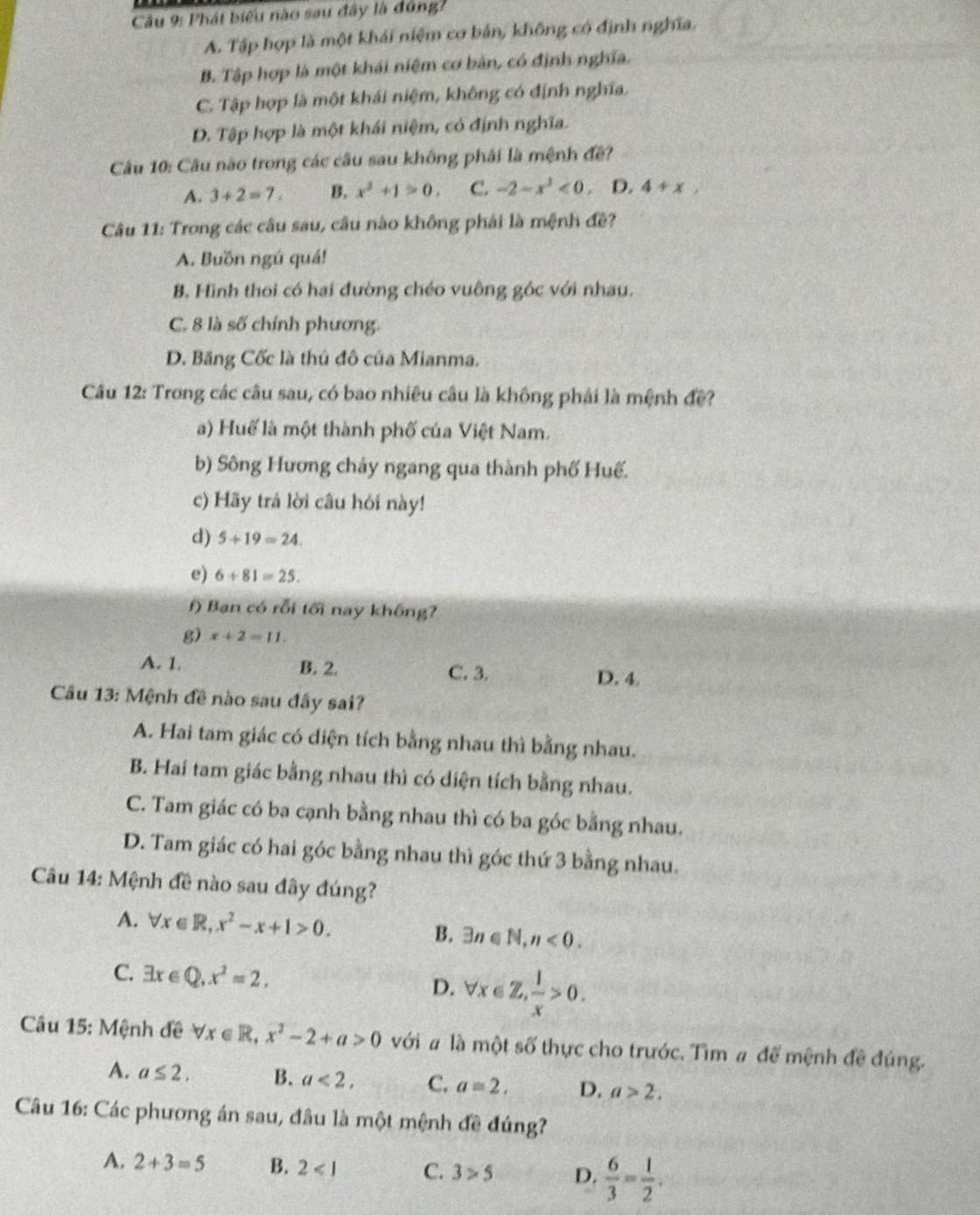









 giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn