Đặt \(A=1+\dfrac{1}{3}+\dfrac{1}{9}+...+\dfrac{1}{729}+\dfrac{1}{2187}\)
=>\(A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^6}+\dfrac{1}{3^7}\)
=>\(3A=3+1+\dfrac{1}{3}+...+\dfrac{1}{3^5}+\dfrac{1}{3^6}\)
=>\(3A-A=3+1+\dfrac{1}{3}+...+\dfrac{1}{3^5}+\dfrac{1}{3^6}-1-\dfrac{1}{3}-...-\dfrac{1}{3^7}\)
=>\(2A=3-\dfrac{1}{3^7}=\dfrac{3^8-1}{3^7}\)
=>\(A=\dfrac{3^8-1}{3^7\cdot2}\)
giúp mik giải bài này nha các bạn
Dãy số tự nhiên liên tiếp 1,2,3,4,5,...,2012 có bao nhiêu chữ số 3 ? (ghi hộ cả cách giải ra hộ mik nhé ) !!!!
Cho mik hỏi là tại sao lại đổi từ 2 giờ 16 phút ra 34/15 vậy các bn. Mik cần gấp . Giải ra hộ mik nhé . Thank
tỉ số phần trăm của :
a)0,45
b)7,43
Giải ra hộ mik nhé!!><
1 a) determine the number of fractions that have the sum of numerator and denominator equal to 2017 .
Các bạn giải ra bằng tiếng anh hộ mik nhé , mong các bạn giải cho mik
giải hộ mik nhé
các bạn giải hộ mik nhé mik sẽ tick giả thik hộ mik luôn
235,05 x 4,2= 9,125 : 2,5
GIẢI HỘ MIK NHÉ ! GIẢI CẢ TẤT!!!!!!!!!!!!!!!!!!!!!!!!
giải hộ mình kĩ càng ra nhé
cho phân số 61 /247 , tìm số tự nhiên a , biết khi bớt a ở mẫu và giữ nguyên tử số , ta đc phân số mới có giá trị bằng 1/4 ?
cảm ơn các bn đã giải hộ mik nhé
A=1,3 - 3,2 + 5,1 -7 + 8,9 -....+ 43,1
giải hộ mik nhé
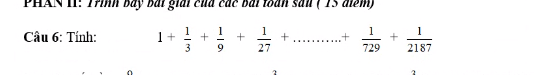giải ra hộ mik nhé
