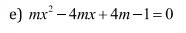`\sqrt{3x+1}+\sqrt{x+1}=8(x>=-1/3)`
`(\sqrt{3x+1}+\sqrt{x+1})^2=8^2`
`3x+1+x+1+2\sqrt{(3x+1)(x+1)}=64`
`4x+2+2\sqrt{(3x+1)(x+1)}=64`
`2x+1+\sqrt{(3x+1)(x+1)}=32`
`\sqrt{(3x+1)(x+1)}=31-2x(x>=31/2)`
`(3x+1)(x+1)=(31-2x)^2`
`3x^2+3x+x+1=4x^2-124x+961`
`x^2-128x+960=0`
`(x^2-8x)+(-120x+960)=0`
`x(x-8)-120(x-8)=0`
`(x-120)(x-8)=0`
`x-120=0` hoặc `x-8=0`
`x=120(L)` hoặc `x=8(tm)`
Vậy: `x=8`
Bài 1: Cho pt x2 + 13x -1 = 0 (1). Không giải pt, hãy lập một pt bậc hai có các nghiệm y1, y2 lớn hơn nghiệm của pt (1) là 2.
Bài 2: Cho pt x2 - 5x + 6 = 0 (1). Không giải pt, hãy lập pt bậc hai có các nghiệm y1 và y2 là:
a/ Số đối các nghiệm của pt (1).
b/ Nghịch đảo các nghiệm của pt (1).
Cho pt X^2+2(m-1)x+m^2=0
1) Giải pt khi m=4
2) Giải pt khi m=-4
giải pt sau để pt vô nghiệm
Cho pt bậc 2 ẩn x: x2 + 3x + m = 0. a) Giải pt (1) khi m = 0; m = -4. b) Tìm m để pt (1) vô nghiệm. c) Tìm m để pt (1) có một nghiệm là -1. Tìm nghiệm kia. d) Cho x1, x2 là 2 nghiệm của pt (1). Không giải pt, hãy tìm giá trị của m để: 1/ x1^2 + x2^2=34 2/ x1 - x2=6 3/ x1=2x2 4/ 3x1+2x2=20 5/ x1^2-x2^2=30.
cho pt x2 -4x+3m-2=o
a) giải pt vs m=1
b)tìm m để giải pt vô nghiệm
c)tìm m để pt có 2 nghiệm trái dấu
lớp 10 nha giúp mk
Cho PT: 2x² - ( 2m +1 )x + m² - 9m + 39 = 0 a) Giải PT khi m = 9 b) Tìm m để PT có 2 nghiệm x1,x2 mà x1 = 2x2 mọi người cho mik công thức câu b) thôi nha mà giải cũng đc
undefined cho pt :(m-1)x^2+2x+1=0 -
giải pt với m =-1 -tìm m để pt có 2 nghiệm phân biệt x1=2x2
Cho pt x²+2x-8=0 gọi x1;x2 là hai nghiệm của pt. Không giải pt mà tính. M=x1(1–x2)+x2(1–x1)
cho pt x2 - 2mx - 2m - 6 =0
a) giải pt khi m=1
b) xác định m để pt có hai nghiệm sao cho x12 + x22 nhỏ nhất
1 cho hệ pt : { x+my=3
{mx + y = 1
a , giải hệ pt khi m=1
b, tìm m để hệ pt có nghiệm duy nhất
2 giải pt 1/x^2-1+ 5/x+1 - 1/x-1 = 1
