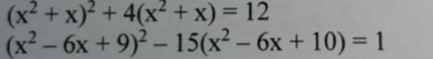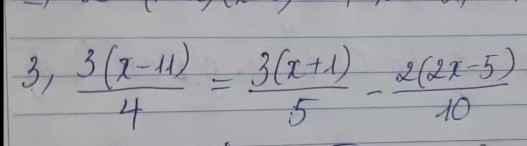1) Đặt \(t=x^2+x\) . P/t : \(t^2+4t=12\Leftrightarrow\left(t+6\right)\left(t-2\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=-6\\t=2\end{matrix}\right.\)
hay \(\left[{}\begin{matrix}x^2+x=-6\\x^2+x=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x^2+x+6=0\left(PTVN\right)\\x^2+x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\) .
2) Đặt \(t=x^2-6x+9=\left(x-3\right)^2\ge0\)
P/t : \(t^2-15\left(t+1\right)=1\) \(\Leftrightarrow t^2-15t-16=0\) \(\Leftrightarrow\left(t-16\right)\left(t+1\right)=0\)
\(\Leftrightarrow t=16\) hay \(\left(x-3\right)^2=16\) \(\Leftrightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)