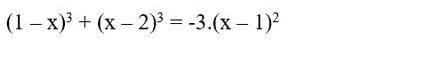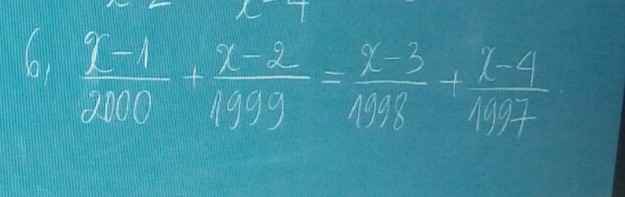\(PT\Leftrightarrow\left(\dfrac{x-1}{2000}-1\right)+\left(\dfrac{x-2}{1999}-1\right)=\left(\dfrac{x-3}{1998}-1\right)+\left(\dfrac{x-4}{1997}-1\right)\\ \Leftrightarrow\dfrac{x-2001}{2000}+\dfrac{x-2001}{1999}=\dfrac{x-2001}{1998}+\dfrac{x-2001}{1997}\\ \Leftrightarrow\left(x-2001\right)\left(\dfrac{1}{2000}+\dfrac{1}{1999}-\dfrac{1}{1998}-\dfrac{1}{1997}\right)=0\\ \Leftrightarrow x=2001\left(\dfrac{1}{2000}+\dfrac{1}{1999}-\dfrac{1}{1998}-\dfrac{1}{1997}\ne0\right)\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Giải pt: Giải pt: ( x-2)^4 - x^4 = y^3
cho pt : \(\dfrac{3x+2}{x-4}=2\)
a. tìm điều kiện xác định pt
b. Giải pt
BÀi 1:Cho PT ẩn x :(5a-8)x=2014
a)Với giá trị nào của a thì PT(1) là PT bậc nhất.
b)Giải PT khi a=2
Bài 2.Tìm giá trị nhỏ nhất:
f(x)=2x2-12x+14
Các bạn giải dùm mình nha,cảm ơn các bạn
\(Giải pt\)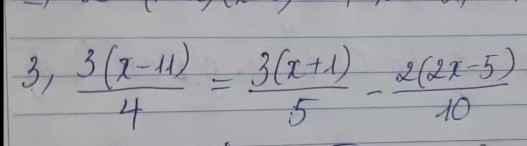
Giải pt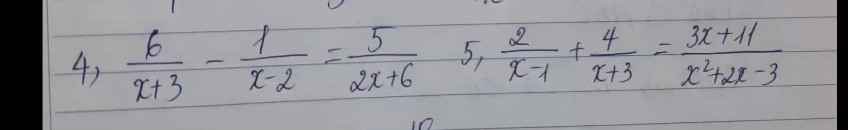
Giải pt
Giải pt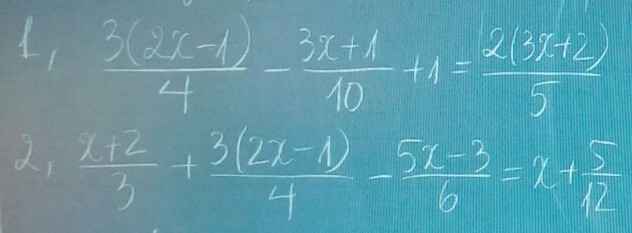
Giải pt
Giải pt