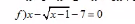ĐKXĐ:\(x-1\ge0\Rightarrow x\ge1\)
\(x-\sqrt{x-1}-7=0\\ \Leftrightarrow\sqrt{x-1}=x-7\left(x\ge7\right)\\ \Leftrightarrow x-1=x^2-14x+49\\ \Leftrightarrow x^2-15x+50=0\\ \Leftrightarrow\left(x^2-10x\right)-\left(5x-50\right)=0\\ \Leftrightarrow x\left(x-10\right)-5\left(x-10\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=10\left(tm\right)\\x=5\left(ktm\right)\end{matrix}\right.\)
f) ĐKXĐ : \(x\ge1\)
\(x-\sqrt{x-1}-7=0\)
<=>\(x-1-3\sqrt{x-1}+2\sqrt{x-1}-6=0\)
<=> \(\left(\sqrt{x-1}-3\right)\left(\sqrt{x-1}+2\right)=0\)
<=> \(\left[{}\begin{matrix}\sqrt{x-1}=3\\\sqrt{x-1}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x\in\varnothing\end{matrix}\right.\Leftrightarrow x=10\)
Vậy x = 10 là nghiệm phương trình