12:
\(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{5}\right)...\left(1-\dfrac{1}{2004}\right)\)
\(B=\left(\dfrac{2}{2}-\dfrac{1}{2}\right)\left(\dfrac{3}{3}-\dfrac{1}{3}\right)\left(\dfrac{4}{4}-\dfrac{1}{4}\right)...\left(\dfrac{2004}{2004}-\dfrac{1}{2004}\right)\)
\(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot\dfrac{4}{5}...\cdot\dfrac{2003}{2004}\)
\(B=\dfrac{1\cdot2\cdot3\cdot...\cdot2002\cdot2003}{2\cdot3\cdot4\cdot...\cdot2003\cdot2004}\)
\(B=\dfrac{1}{2004}\)
`12) B=(1-1/2)(1-1/3)(1-1/4)(1-1/5)....(1-1/2003)(1-1/2004)`
`B=1/2 . 2/3 . 3/4 . 4/5 .... 2002/2003 . 2003/2004`
`B= [1.2.3.4......2002.2003]/[2.3.4.5.....2003.2004]`
`B=1/2004`
`7)`
`a)[254xx399-145]/[254+399xx253]`
`=[(253+1)xx399-145]/[254+399xx253]`
`=[253xx399+399-145]/[254+399xx253]`
`=[254+253xx399]/[254+253xx399]=1`
`b)[5932+6001xx5931]/[5932xx6001-69]`
`=[5932+6001xx5931]/[(5931+1)xx6001-69]`
`=[5932+6001xx5931]/[5931xx6001+6001-69]`
`=[5932+6001xx5931]/[5932+6001xx5931]=1`

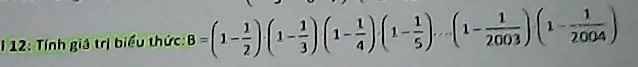
 Giải hộ tớ nhé đang gấp :00
Giải hộ tớ nhé đang gấp :00













 các cậu giải hộ tớ bài này nhé cảm ơn cac cậu
các cậu giải hộ tớ bài này nhé cảm ơn cac cậu