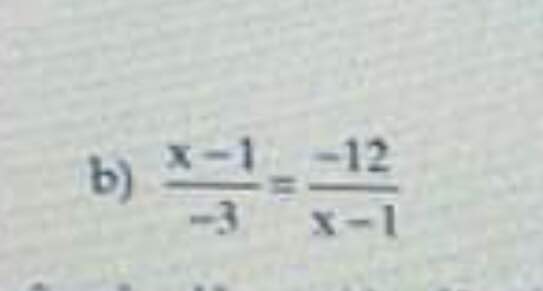Bài 2:
Các cặp góc so le trong là: \(\hat{A_4};\hat{B}_2\) ; \(\hat{A_3};\hat{B_1}\)
Các cặp góc đồng vị là: \(\hat{A_1};\hat{B_1}\) ; \(\hat{A_2};\hat{B_2}\) ; \(\hat{A_3};\hat{B_3}\) ; \(\hat{A_4};\hat{B_4}\)
Bài 3:
a: Các cặp góc so le trong là: \(\hat{P_1};\hat{Q_3}\) ; \(\hat{P_2};\hat{Q_4}\)
Các cặp góc đồng vị là: \(\hat{P_1};\hat{Q_1}\) ; \(\hat{P_2};\hat{Q_2}\) ; \(\hat{P_3};\hat{Q_3}\) ; \(\hat{P_4};\hat{Q_4}\)
b: Ta có: \(\hat{P_4}+\hat{P_3}=180^0\) (hai góc kề bù)
=>\(\hat{P_3}=180^0-32^0=148^0\)
Ta có: \(\hat{P_4}=\hat{P_2}\) (hai góc đối đỉnh)
mà \(\hat{P_4}=32^0\)
nên \(\hat{P_2}=32^0\)
Ta có: \(\hat{P_3}=\hat{P_1}\) (hai góc đối đỉnh)
mà \(\hat{P_3}=148^0\)
nên \(\hat{P_1}=148^0\)
Ta có: \(\hat{Q_2}+\hat{Q_3}=180^0\) (hai góc kề bù)
=>\(\hat{Q_3}=180^0-32^0=148^0\)
Ta có: \(\hat{Q_1}=\hat{Q_3}\) (hai góc đối đỉnh)
mà \(\hat{Q_3}=148^0\)
nên \(\hat{Q_1}=148^0\)
Ta có: \(\hat{Q_2}=\hat{Q_4}\) (hai góc đối đỉnh)
mà \(\hat{Q_2}=32^0\)
nên \(\hat{Q_4}=32^0\)
c: Ta có: \(\hat{P_1}=148^0;\hat{Q_3}=148^0\)
Do đó: \(\hat{P_1}=\hat{Q_3}\)
\(\hat{P_2}=32^0;\hat{Q_4}=32^0\)
=>\(\hat{P_2}=\hat{Q_4}\)
Ta có: \(\hat{P_3}=148^0;\hat{Q_3}=148^0\)
=>\(\hat{P_3}=\hat{Q_3}\left(=148^0\right)\)
Ta có \(\hat{P_4}=32^0;\hat{Q_4}=32^0\)
Do đó: \(\hat{P_4}=\hat{Q_4}\)
Ta có: \(\hat{P_2}=32^0;\hat{Q_2}=32^0\)
Do đó: \(\hat{P_2}=\hat{Q_2}\)
Ta có: \(\hat{P_1}=148^0;\hat{Q_1}=148^0\)
=>\(\hat{P_1}=\hat{Q_1}\left(=148^0\right)\)
Nhận xét: Các cặp góc so le trong và các cặp góc đồng vị đều bằng nhau








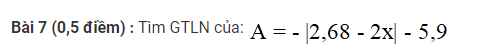

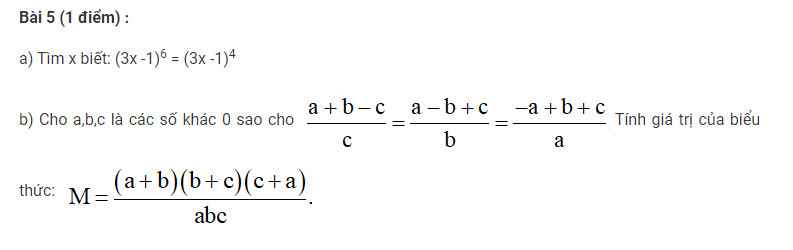 giải hộ bài này với ạ
giải hộ bài này với ạ