\(\)với \(x\ge0,x\ne4\)
\(=>B=\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\right]:\dfrac{3}{\sqrt{x}+1}\)
\(B=\left[\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\right].\dfrac{\sqrt{x}+1}{3}\)
\(B=\dfrac{3.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)3}=\dfrac{1}{\sqrt{x}-2}\)
\(=>P=\dfrac{18}{A.B}=\dfrac{18}{\dfrac{x-4}{\sqrt{x}-1}.\dfrac{1}{\sqrt{x}-2}}=\dfrac{18}{\dfrac{\sqrt{x}+2}{\sqrt{x}-1}}\)
\(=\dfrac{18\left(\sqrt{x}-1\right)}{\sqrt{x}+2}\)\(=\dfrac{18\sqrt{x}-18}{\sqrt{x}+2}=\dfrac{18\sqrt{x}}{\sqrt{x}+2}-\dfrac{18}{\sqrt{x}+2}\ge-9\)
dấu"=" xảy ra<=>x=0(tm)
\(\)
mọi ng hộ e câu 6 vs câu 9 vs ạ
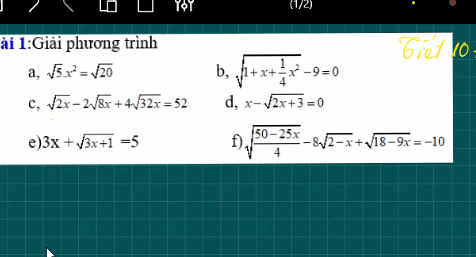
giải hộ mình vs ạ mình cần gấp ạ
