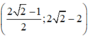Xét (I): 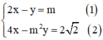
Từ phương trình (1) ta rút ra được y = 2x – m (*)
Thay (*) vào phương trình (2) ta được:
4x – m2.(2x – m) = 2√2
⇔ 4x – 2m2.x + m3 = 2√2
⇔ (4 – 2m2).x = 2√2 – m3 (**)
a) Với m = -√2, phương trình (**) trở thành: 0x = 4√2
Phương trình vô nghiệm.
Vậy với m = -√2, hệ phương trình (I) vô nghiệm.
b) Với m = √2, phương trình (**) trở thành: 0x = 0
Phương trình nghiệm đúng với mọi x ∈ R, khi đó y = 2x – √2
Vậy với m = √2, hệ (I) có vô số nghiệm dạng (x ; 2x - √2), x ∈ R
c) Với m = 1, phương trình (**) trở thành: 2x = 2√2 – 1 ⇔ 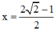
Thay vào (*) ta được:
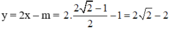
Vậy hệ phương trình có nghiệm duy nhất