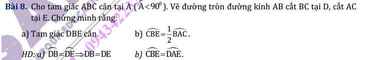a: \(P=\dfrac{2\sqrt{x}-9-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-x+2\sqrt{x}+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Để P<1 thì P-1<0
\(\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
hay x<9
Kết hợp ĐKXĐ, ta được: 0<=x<9 và x<>4
c: Để P<1 thì 0<=x<9 và x<>4
mà x là số nguyên
nên \(x\in\left\{0;1;2;3;5;6;7;8\right\}\)

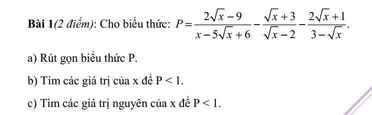







 cảm ơn
cảm ơn