1:
a: Phương trình hoành độ giao điểm là:
\(-x^2=mx+2\)(1)
=>\(x^2+mx+2=0\)
\(\text{Δ}=m^2-4\cdot1\cdot2=m^2-8\)
Để (P) cắt (d) tại 1 điểm duy nhất thì phương trình (1) có 1 nghiệm duy nhất
=>Δ=0
=>\(m^2-8=0\)
=>\(m^2=8\)
=>\(m=\pm2\sqrt{2}\)
b: Thay x=-2 và y=m vào (P), ta được:
\(m=-\left(-2\right)^2=-4\)
Thay x=1 và y=n vào (d), ta được:
\(m\cdot1+2=n\)
=>-4+2=n
=>n=-2
2:
Gọi chiều dài hình chữ nhật đã cho là x(m)
(Điều kiện: x>2)
Chiều rộng hình chữ nhật đã cho là 0,5x(m)
Chiều dài hình chữ nhật khi giảm đi 2m là x-2(m)
Chiều rộng hình chữ nhật khi giảm đi 2m là 0,5x-2(m)
Diện tích ban đầu là \(0,5x\cdot x=0,5x^2\left(m^2\right)\)
Diện tích lúc sau là: \(\left(x-2\right)\cdot\left(0,5x-2\right)=0,5x^2-3x+4\left(m^2\right)\)
Diện tích lúc sau giảm đi một nửa nên ta có:
\(0,5x^2-3x+4=0,5\cdot0,5x^2=0,25x^2\)
=>\(0,25x^2-3x+4=0\)
=>\(x^2-12x+16=0\)
=>\(\left[{}\begin{matrix}x=6+2\sqrt{5}\left(nhận\right)\\x=6-2\sqrt{5}\left(loại\right)\end{matrix}\right.\)
vậy: Chiều dài ban đầu của hình chữ nhật là \(6+2\sqrt{5}\left(m\right)\)





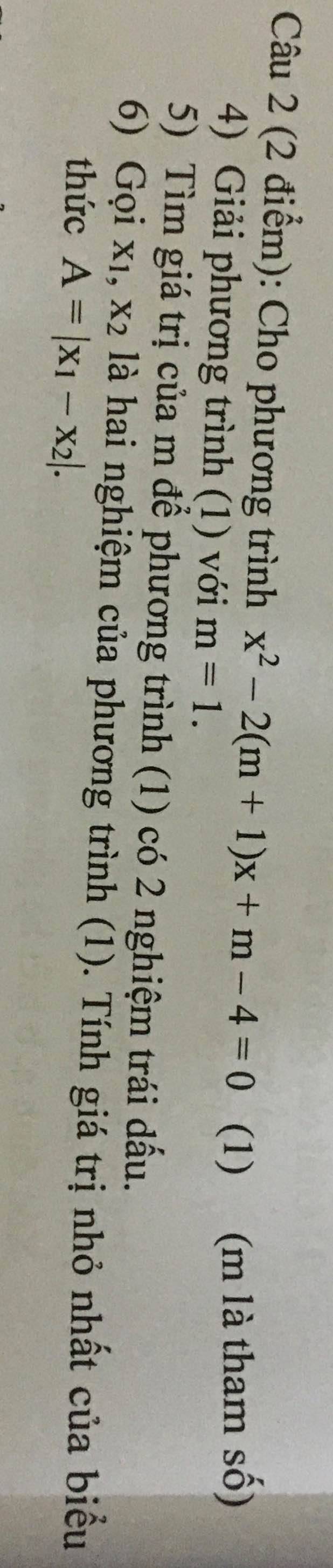

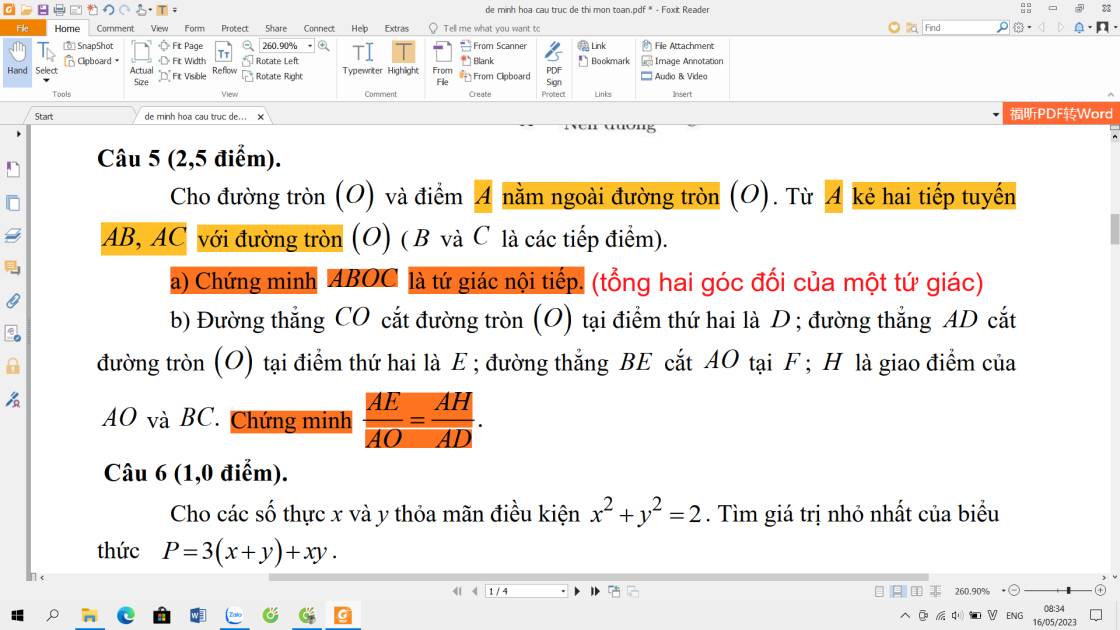 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ








