Bài 1 :
d) \(\dfrac{1}{x-1}+\dfrac{2}{x-2}=\dfrac{6}{x-6}+\dfrac{1}{x-3}\left(x\ne\left\{1;2;3;6\right\}\right)\)
\(\Leftrightarrow\left(\dfrac{1}{x-1}+1\right)+\left(\dfrac{2}{x-2}+1\right)-\left(\dfrac{1}{x-3}+1\right)-\left(\dfrac{6}{x-6}+1\right)=0\)
\(\Leftrightarrow\left(\dfrac{x}{x-1}\right)+\left(\dfrac{x}{x-2}\right)-\left(\dfrac{x}{x-3}\right)-\left(\dfrac{x}{x-6}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-3}-\dfrac{1}{x-6}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-3}-\dfrac{1}{x-6}\right)=0\)
mà \(\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-3}-\dfrac{1}{x-6}\ne0\) vì \(\dfrac{1}{x-1}+\dfrac{2}{x-2}=\dfrac{6}{x-6}+\dfrac{1}{x-3}\)
\(\Leftrightarrow x=0\)
Bài 35 :
d) \(\dfrac{x+1}{x^2+x+1}-\dfrac{x-1}{x^2-x+1}=\dfrac{3}{x\left(x^4+x^2+1\right)}\left(1\right)\left(x\ne0\right)\)
Ta thấy :
\(\left(x^2+x+1\right)\left(x^2-x+1\right)=\left(x^2+1+x\right)\left(x^2+1-x\right)=\left(x^2+1\right)^2-x^2\)
\(=x^4+2x^2+1-x^2=x^4+x^2+1\)
Nên Ta lấy mẫu số chung của phương trình trên là \(x\left(x^4+x^2+1\right)\)
\(\left(1\right)\Leftrightarrow\dfrac{x\left(x+1\right)\left(x^2-x+1\right)-x\left(x-1\right)\left(x^2+x+1\right)-3}{x\left(x^4+x^2+1\right)}=0\)
\(\Leftrightarrow x\left(x^3+1\right)-x\left(x^3-1\right)-3=0\)
\(\Leftrightarrow x^4+x-x^4+x-3=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=\dfrac{3}{2}\left(tm\right)\)
Vậy \(x=\dfrac{3}{2}\) là nghiệm phương trình (1)

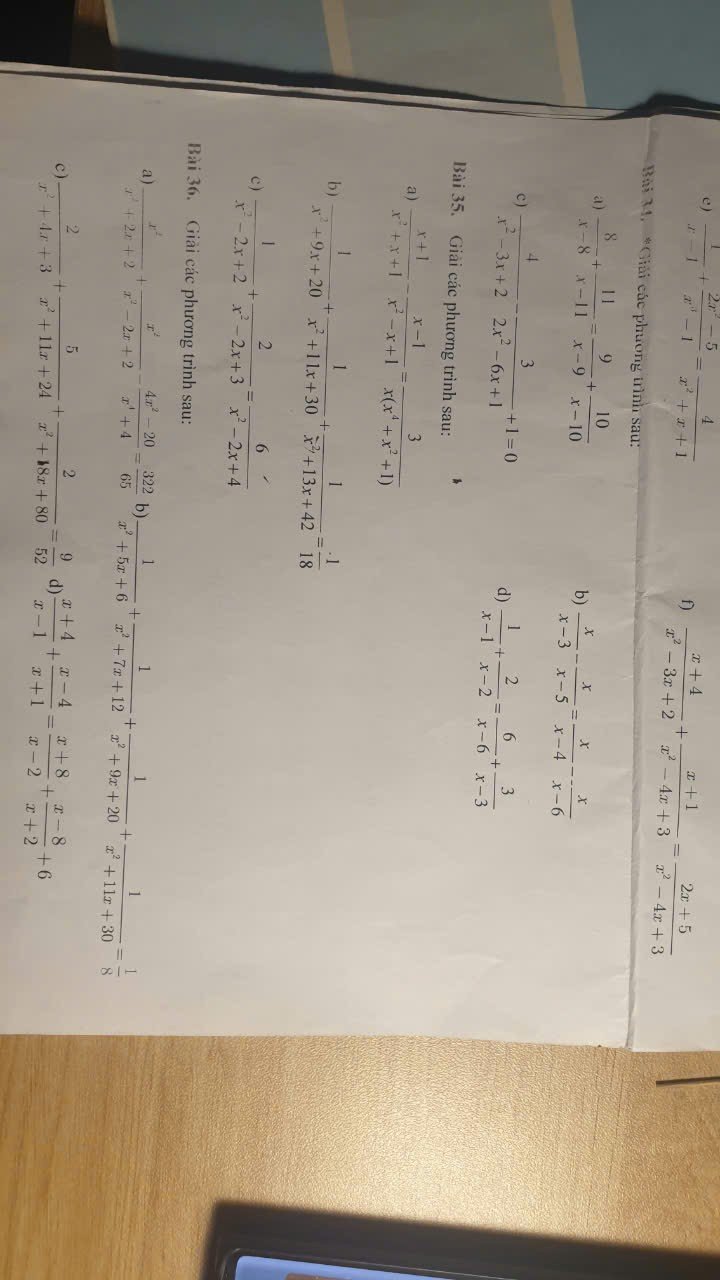









 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn















