\(\text{#TNam}\)
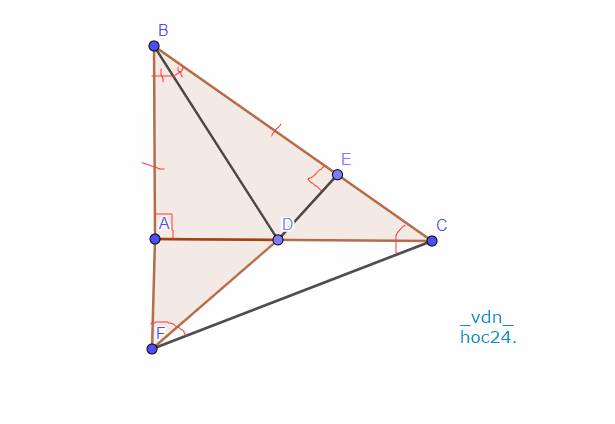
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`AB = EB (g``t)`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\) \(\widehat{ABE})\)
`\text {BD chung}`
`=> \text {Tam giác ABD = Tam giác EBD (c-g-c)}`
`->`\(\widehat{BAD}=\widehat{BED} (\text {2 góc tương ứng})\)
Mà \(\widehat{BAD}=90^0\)
`->`\(\widehat{BAD}=\widehat{BED}=90^0\)
`->`\(\widehat{BED}\) \(\text {là góc vuông}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`BA = BE (g``t)`
\(\widehat{B}\) \(\text {chung}\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Xét Tam giác `BFC:`
`BF = BC (CMT)`
`-> text {Tam giác BFC cân tại B}`
`c,`
Vì Tam giác `BFC` cân tại `B`
`->`\(\widehat{F}=\widehat{C}\)
Xét Tam giác `AFC` và Tam giác `ECF` có:
\(\widehat{F}=\widehat{C}\)
`\text {FC chung}`
\(\widehat{CAF}=\widehat{FEC}=90^0\)
`=> \text {Tam giác AFC = Tam giác ECF (ch-gn)}`