\(\widehat{CAD}+\widehat{DAB}=180^0\)(hai góc kề bù)
=>\(\widehat{DAB}+63^0=180^0\)
=>\(\widehat{DAB}=117^0\)
Xét ΔDAB có \(\widehat{DAB}+\widehat{DBA}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}+117^0+48^0=180^0\)
=>\(\widehat{ADB}=15^0\)
Xét ΔDAB có \(\dfrac{AB}{sinADB}=\dfrac{AD}{sinB}\)
=>\(\dfrac{24}{sin15}=\dfrac{AD}{sin48}\)
=>\(AD\simeq68,91\left(m\right)\)
Xét ΔCAD vuông tại C có \(CD=AC\cdot sinDAC\)
=>\(h\simeq68,91\cdot sin63\simeq61,4\left(m\right)\)
Đúng 1
Bình luận (0)
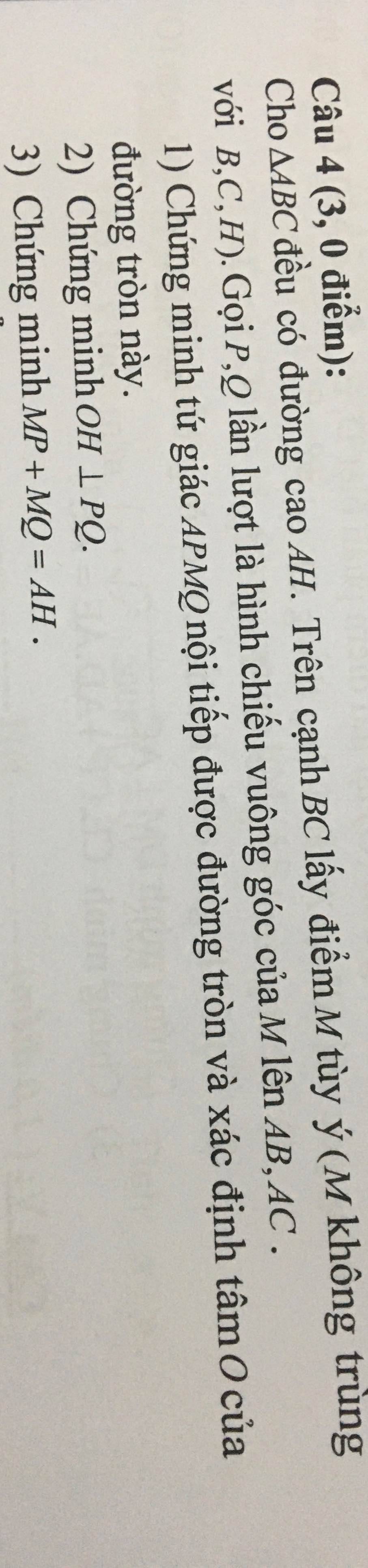
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
