a: \(A=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b: Để 2/A là số nguyên thì \(2\sqrt{a}⋮\sqrt{a}-1\)
\(\Leftrightarrow\sqrt{a}-1\in\left\{1;-1;2;-2\right\}\)
hay \(a\in\left\{4;0;9\right\}\)
`a)`\(A=\left(\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\)
\(ĐK:\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
\(A=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(A=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
`b)`\(\dfrac{2}{A}=\dfrac{2\sqrt{a}}{\sqrt{a}-1}\)
\(=\dfrac{2\left(\sqrt{a}-1\right)+2}{\sqrt{a}-1}=2+\dfrac{2}{\sqrt{a}-1}\)
Để nhận giá trị nguyên thì \(\sqrt{a}-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
`@`\(\sqrt{a}-1=1\Rightarrow a=4\left(tm\right)\)
`@`\(\sqrt{a}-1=-1\Rightarrow a=0\left(ktm\right)\)
`@`\(\sqrt{a}-1=2\Rightarrow a=9\left(tm\right)\)
`@`\(\sqrt{a}-1=-2\Rightarrow\) vô lý
Vậy \(a\in\left\{4;9\right\}\) thì đạt g.trị nguyên
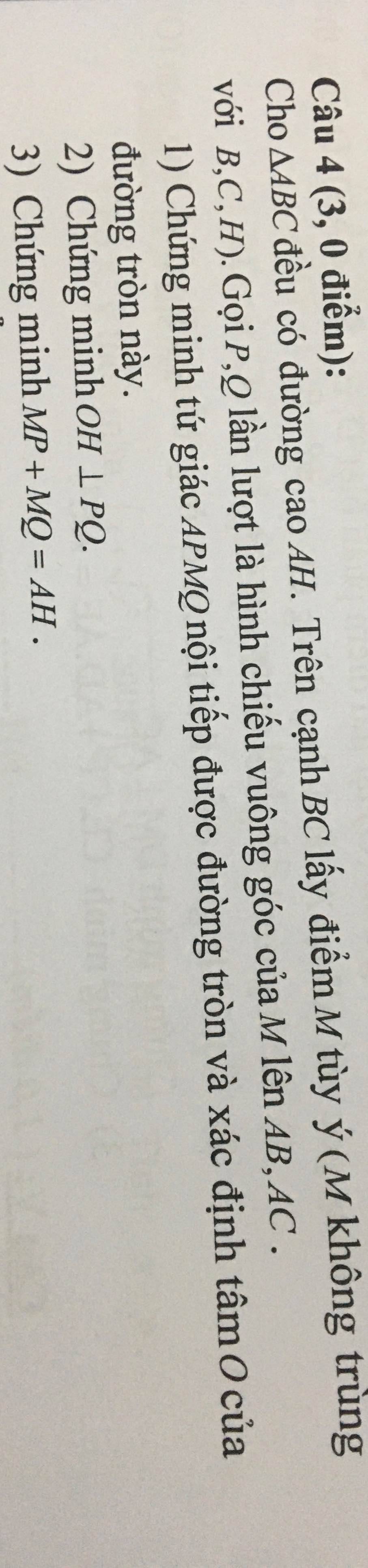
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
