Question

 giải giúp e với e cần gấp ạ

Answer 1

Lời giải:
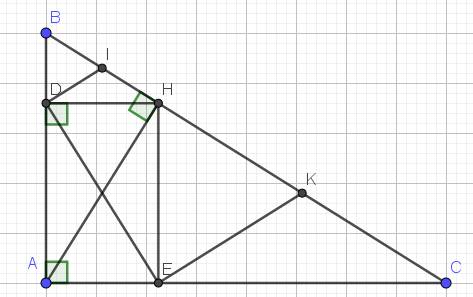
a. Xét tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên tứ giác $ADHE$ là hình chữ nhật.

b.

Xét tam giác vuông $BDH$ vuông tại $D$ có $DI$ là đường trung tuyến ứng với cạnh huyền $BH$ nên $DI=\frac{BH}{2}=IH$

$\Rightarrow DIH$ là tam giác vuông tại $I$

$\Rightarrow \widehat{IDH}=\widehat{IHD}$ (1)

$ADHE$ là hình chữ nhật nên $\widehat{HDE}=\widehat{HAE}=\widehat{HAC}$ (2)

Từ $(1); (2)\Rightarrow \widehat{IDH}+\widehat{HDE}=\widehat{IHD}+\widehat{HAC}$

$\Rightarrow \widehat{IDE}=\widehat{IHD}+\widehat{HAC}$.

Mà $\widehat{IHD}=\widehat{HCA}$ (2 góc đồng vị)

$\Rightarrow \widehat{IDE}=\widehat{HCA}+\widehat{HAC}=180^0-\widehat{AHC}=180^0-90^0=90^0$

$\Rightarrow DI\perp DE$

c. Tương tự phần a ta suy ra $DE\perp EK$

Vậy $DI\perp DE, EK\perp DE$

$\Rightarrow DI\parallel EK$ và $DI, EK$ cùng vuông góc với $DE$

$\Rightarrow DIKE$ là hình thang vuông.

d.

Có: $DI=\frac{BH}{2}\Rightarrow BH=2DI=2.1=2$ (cm) 

$EK=\frac{CH}{2}\Rightarrow CH=2EK=8$ (cm)

$\Rightarrow BC=BH+CH=2+8=10$ (cm)

$S_{ABC}=AH.BC:2=6.10:2=30$ (cm²)

Answer 2

Hình vẽ: