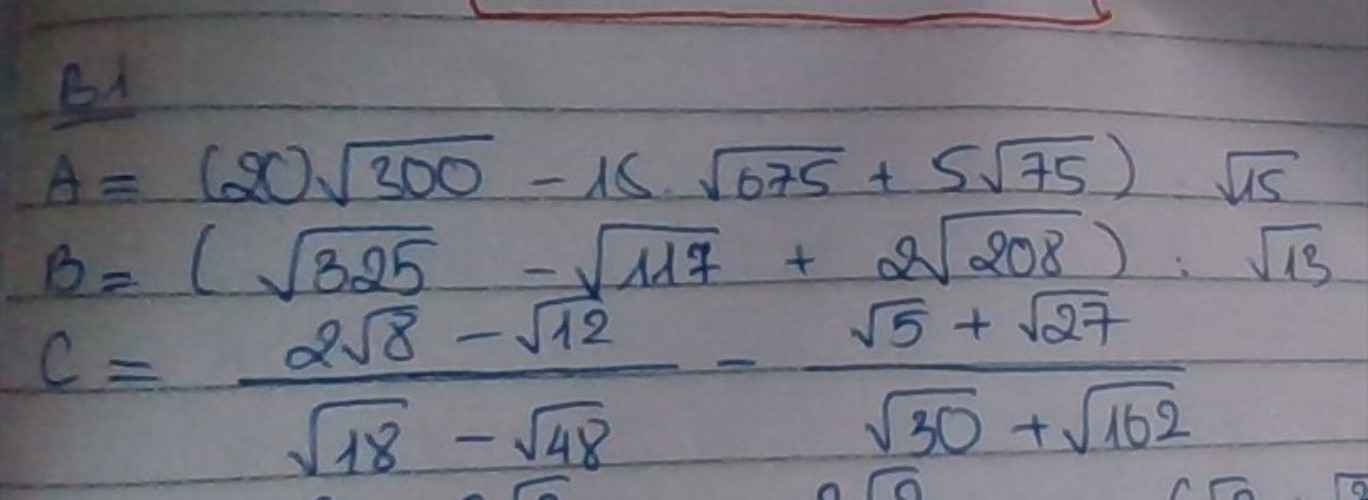\(A=\left(20\sqrt{300}-15\sqrt{675}+5\sqrt{75}\right):\sqrt{15}\\ \Leftrightarrow A=\left(200\sqrt{3}-225\sqrt{3}+25\sqrt{3}\right):\sqrt{15}\\ \Leftrightarrow A=0:\sqrt{15}=0\)
\(B=\left(\sqrt{325}-\sqrt{117}+2\sqrt{208}\right):\sqrt{13}\\ \Leftrightarrow B=\left(5\sqrt{13}-3\sqrt{13}+8\sqrt{13}\right):\sqrt{13}\\ \Leftrightarrow B=10\sqrt{13}:\sqrt{13}=10\)
c: Ta có: \(C=\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\dfrac{-2\left(\sqrt{3}-2\sqrt{2}\right)}{\sqrt{6}\left(\sqrt{3}-2\sqrt{2}\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}\)
\(=\dfrac{-3}{\sqrt{6}}=-\dfrac{\sqrt{6}}{2}\)