Bài 1
a) Do MA là tia phân giác của ∠NMP (gt)
⇒ ∠NMA = ∠PMA
⇒ ∠CMA = ∠DMA
Xét hai tam giác vuông: ∆MAC và ∆MAD có:
MA là cạnh chung
∠CMA = ∠DMA (cmt)
⇒ ∆MAC = ∆MAD (cạnh huyền - góc nhọn)
b) Do ∆MNP cân tại M (gt)
MA là tia phân giác của ∠NMP (gt)
⇒ MA là đường phân giác của ∆MNP
⇒ MA là đường trung trực của ∆MNP
⇒ MA là đường trung trực của NP
c) Do ∆MAC = ∆MAD (cmt)
⇒ MC = MD (hai cạnh tương ứngl
⇒ M nằm trên đường trung trực của CD (1)
Do ∆MAC = ∆MAD (cmt)
⇒ AC = AD (hai cạnh tương ứng)
⇒ A nằm trên đường trung trực của CD (2)
Từ (1) và (2) ⇒ MA là đường trung trực của CD
Bài 2
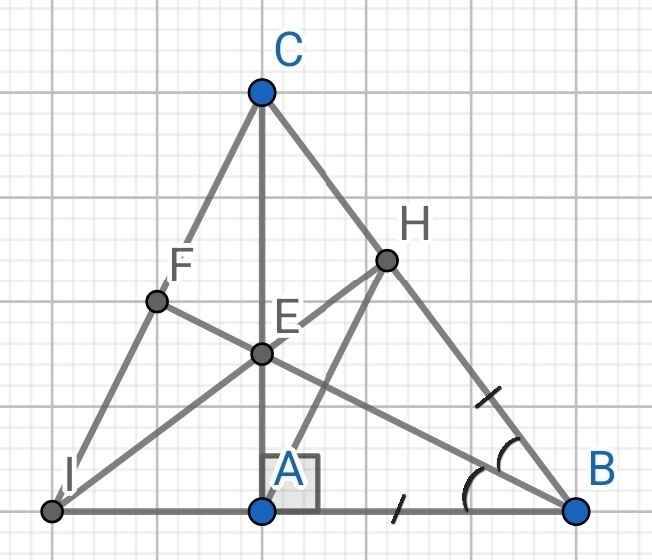
a) Do BE là tia phân giác của ∠ABC (gt)
⇒ ∠ABE = ∠CBE
⇒ ∠ABE = ∠HBE
Xét ∆ABE và ∆HBE có:
AB = BH (gt)
∠ABE = ∠HBE (cmt)
BE là cạnh chung
⇒ ∆ABE = ∆HBE (c-g-c)
b) Do ∆ABE = ∆HBE (cmt)
⇒ ∠BAE = ∠BHE (hai góc tương ứng)
⇒ ∠BHE = 90⁰
⇒ BH ⊥ EH
⇒ EH ⊥ BC
c) Do AB = BH (gt)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABE = ∆HBE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
⇒ E nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BE là đường trung trực của AH
⇒ BE ⊥ AH
d) Xét hai tam giác vuông: ∆ABC và ∆HBI có:
AB = BH (gt)
∠B chung
⇒ ∆ABC = ∆HBI (cạnh góc vuông - góc nhọn kề)
⇒ BC = BI (hai cạnh tương ứng)
⇒ ∆IBC cân tại B
e) ∆BCI có:
CA ⊥ BI (do CA ⊥ AB)
⇒ CA là đường cao của ∆BCI
Do EH ⊥ BC (cmt)
⇒ IH ⊥ BC
⇒ IH là đường cao thứ hai của ∆BCI
Mà E là giao điểm của CA và IH
⇒ BE là đường cao thứ ba của ∆BCI
Mà ∆BCI cân tại B
⇒ BE là đường trung trực của ∆BCI
⇒ BE là đường trung trực của IC
Mà F là trung điểm của IC (gt)
⇒ B, E, F thẳng hàng

 Giải gấp giúp mình ạ
Giải gấp giúp mình ạ



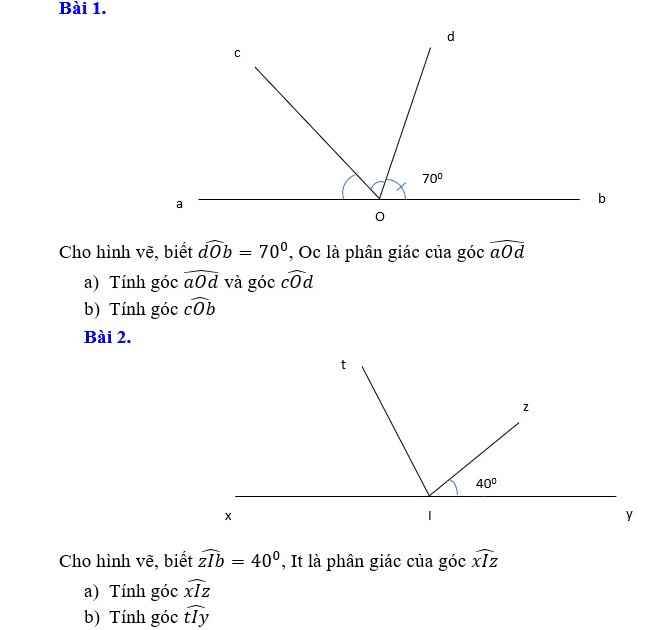
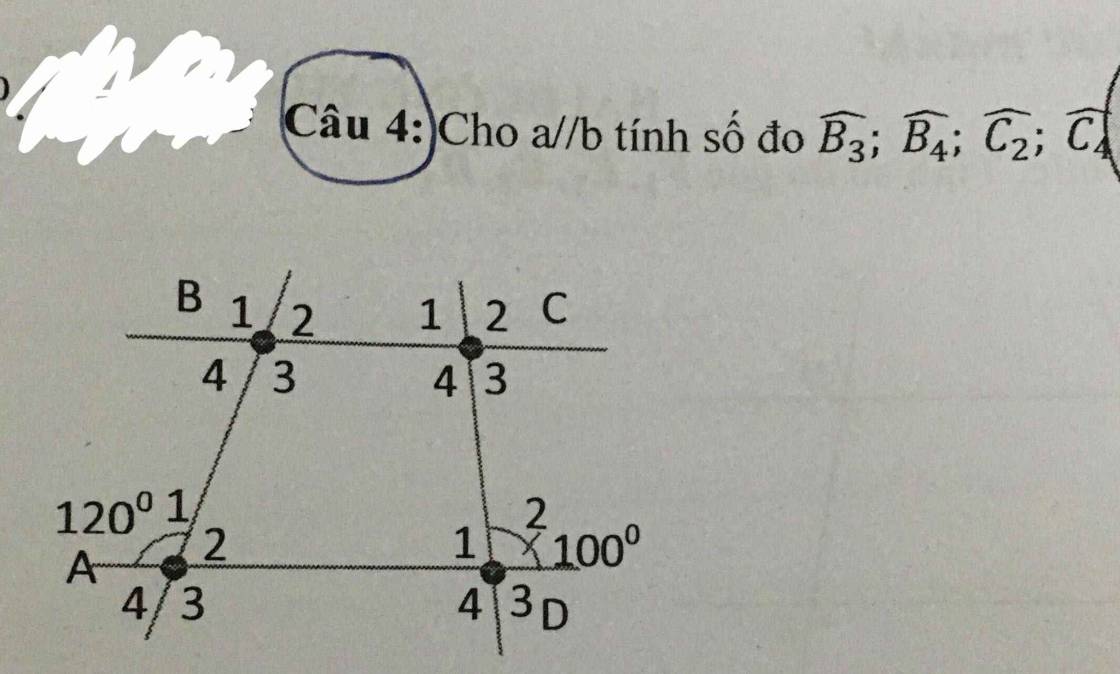
 Mg giải giúp mình ạ mình đang rất gấp
Mg giải giúp mình ạ mình đang rất gấp Mg giải gấp giúp mình ạ
Mg giải gấp giúp mình ạ Mg giải gấp giúp mình ạ
Mg giải gấp giúp mình ạ