5/ \(10x+3-5x\le14x+12\)
<=>\(10x-5x-14x\le12-3\)
<=>\(-9x\le9\)
<=>\(x\ge-1\)
Vậy bất phương trình có nghiệm là \(x\ge-1\)
6/\(\left(3x-1\right)< 2x+4\)
<=>\(3x-2x< 4+1\)
<=> x<5
Vậy tập nghiệm của bất phương trình là x<5
9/ \(\left(x-1\right)\left(x+2\right)>\left(x-1\right)^2+3\)
<=>\(x^2+2x-x-2>x^2-2x+1+3\)
<=> \(x^2+2x-x-x^2-2x>1+3+2\)
<=>\(-x>6\)
<=> x<-6
Vậy nghiệm của bất pt là X<-6
10/ \(x\left(2x-1\right)-8< 5-2x\left(1-x\right)\)
<=> \(2x^2-x-8< 5-2x+2x^2\)
<=>\(2x^2-x-2x^2< 5+8\)
<=> \(-x< 13\)
<=> \(x>-13\)
Vậy pt có nghiệm là x>-13
12/ \(\left(x-4\right)\left(x+4\right)\ge\left(x+3\right)^2+5\)
<=>\(x^2+4x-4x-16\ge x^2+6x+9+5\)
<=> \(x^2+4x-4x-x^2+6x\ge9+5+16\)
<=> \(0\ge30\)
Vậy bất pt vô nghiệm





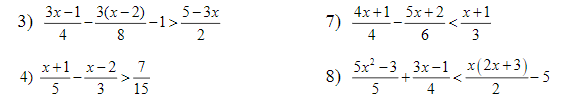

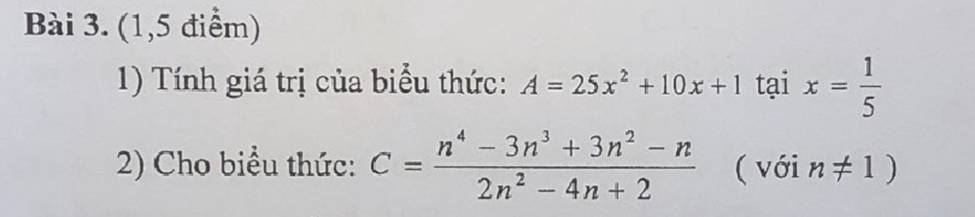 Giải dùm mình với ạ! Mình cần gấp
Giải dùm mình với ạ! Mình cần gấp













