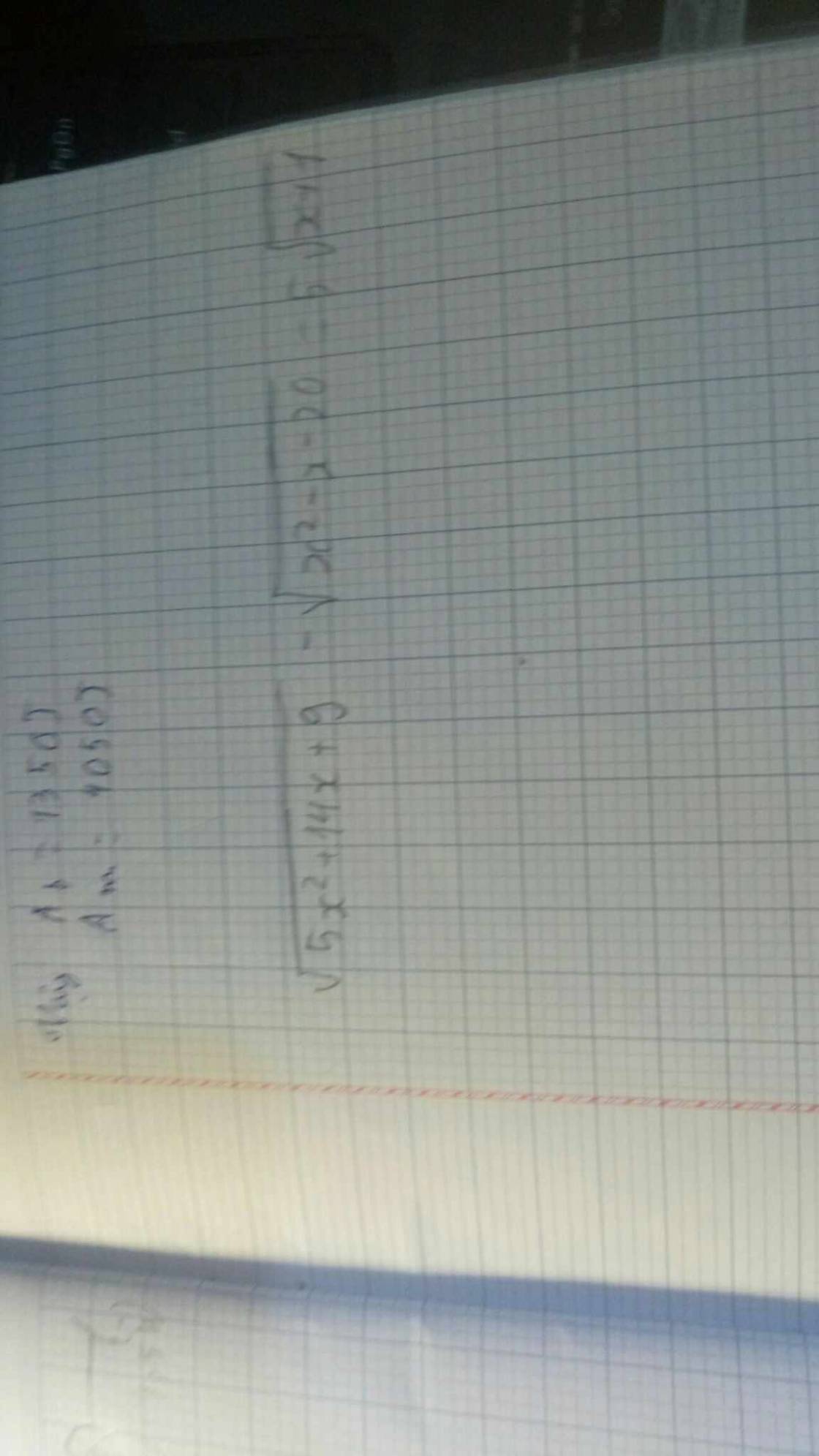
ĐKXĐ: \(\left\{{}\begin{matrix}5x^2+14x+9>=0\\x+1>=0\\x^2-x-20>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+1\right)\left(5x+9\right)>=0\\x+1>=0\\\left(x-5\right)\left(x+4\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< =-\dfrac{9}{5}\\x>=-1\end{matrix}\right.\\x>=-1\\\left[{}\begin{matrix}x>=5\\x< =-4\end{matrix}\right.\end{matrix}\right.\)
=>x>=5
\(\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
=>\(\sqrt{5x^2+14x+9}-21+6-\sqrt{x^2-x-20}=5\sqrt{x+1}-15\)
=>\(\dfrac{5x^2+14x+9-441}{\sqrt{5x^2+14x+9}+21}+\dfrac{36-x^2+x+20}{6+\sqrt{x^2-x-20}}=5\left(\sqrt{x+1}-3\right)\)
=>\(\dfrac{5x^2+14x-432}{\sqrt{5x^2+14x+9}+21}+\dfrac{-x^2+x+56}{6+\sqrt{x^2-x-20}}=5\cdot\dfrac{x+1-9}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+54\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{x^2-x-56}{\sqrt{x^2-x-20}+6}=\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+4\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{\left(x-8\right)\left(x+7\right)}{\sqrt{x^2-x-20}+6}-\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}=0\)
=>\(\left(x-8\right)\left(\dfrac{5x+4}{\sqrt{5x^2+14x+9}+21}-\dfrac{x+7}{\sqrt{x^2-x-20}+6}-\dfrac{5}{\sqrt{x+1}+3}\right)=0\)
=>x-8=0
=>x=8(nhận)