Bài 1:
a: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{3}\right)\)
nên DE//BC
b: Sửa đề: K là trung điểm của DE
Xét ΔABI có DK//BI
nên \(\dfrac{DK}{BI}=\dfrac{AK}{AI}\left(1\right)\)
Xét ΔACI có KE//CI
nên \(\dfrac{KE}{CI}=\dfrac{AK}{AI}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{DK}{BI}=\dfrac{KE}{CI}\)
mà BI=CI
nên DK=KE
=>K là trung điểm của DE
c: Xét ΔABC có DE//BC
nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)
=>\(\dfrac{DE}{10}=\dfrac{1}{3}\)
=>\(DE=10\cdot\dfrac{1}{3}=\dfrac{10}{3}\left(cm\right)\)
Bài 2:
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{HB}{AB}=\dfrac{HA}{AC}=\dfrac{BA}{BC}\)
=>\(\dfrac{HB}{15}=\dfrac{HA}{20}=\dfrac{15}{25}=\dfrac{3}{5}\)
=>\(HB=15\cdot\dfrac{3}{5}=9\left(cm\right);HA=20\cdot\dfrac{3}{5}=12\left(cm\right)\)
HB+HC=BC
=>HC+9=25
=>HC=16(cm)
b: Xét ΔBAC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{15}=\dfrac{DC}{25}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=20cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{20}{8}=2,5\)
=>\(DA=3\cdot2,5=7,5\left(cm\right);DC=5\cdot2,5=12,5\left(cm\right)\)
c: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó; ΔBAD~ΔBHI
=>\(\dfrac{BA}{BH}=\dfrac{BD}{BI}\)
=>\(BA\cdot BI=BD\cdot BH\)
d: Xét ΔBAH có BI là phân giác
nên \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}\left(2\right)\)
ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)
e: Xét ΔAHC có AK là phân giác
nên \(\dfrac{HK}{KC}=\dfrac{AH}{AC}\left(4\right)\)
ΔBHA~ΔBAC
=>\(\dfrac{AH}{AC}=\dfrac{BH}{BA}\left(5\right)\)
Từ (4),(5),(1) suy ra \(\dfrac{HI}{IA}=\dfrac{HK}{KC}\)
=>IK//AC






 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ
Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ




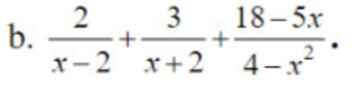 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn



