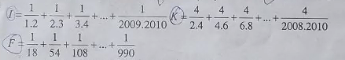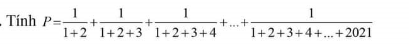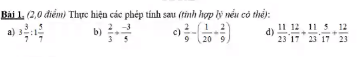\(I=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2009.2010}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2010}\\ =1-\dfrac{1}{2010}\\ =\dfrac{2009}{2010}\)
\(K=\dfrac{4}{2.4}+\dfrac{4}{4.6}+...+\dfrac{4}{2008.2010}\\ =2\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{2008.2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{2010}\right)\\ =2.\dfrac{502}{1005}\\ =\dfrac{1004}{1005}\)
\(F=\dfrac{1}{18}+\dfrac{1}{54}+...+\dfrac{1}{990}\\ =\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{30.33}\\ =\dfrac{1}{3}\left(\dfrac{3}{3.6}+\dfrac{3}{6.9}+...+\dfrac{3}{30.33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}.\dfrac{10}{33}\\ =\dfrac{10}{99}\)
\(I=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2009}-\dfrac{1}{2010}=\dfrac{2010-1}{2010}=\dfrac{2008}{2010}\)
\(K=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}=\dfrac{502}{1005}\)
\(F=\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{99.100}=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{100}\right)=\dfrac{97}{900}\)