Với điều kiện x > 1 ta có phương trình:
ln(4x + 2) = ln[x(x − 1)]
⇔ 4x + 2 = x 2 – x ⇔ x 2 – 5x – 2 = 0
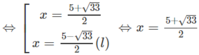
Với điều kiện x > 1 ta có phương trình:
ln(4x + 2) = ln[x(x − 1)]
⇔ 4x + 2 = x 2 – x ⇔ x 2 – 5x – 2 = 0
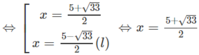
Giải phương trình lnx + ln(x - 1) = ln2
A. x = 3/2
B. x = -1, x = 2
C. x = 2
D. x = 1, x = 3/2
Giải các bất phương trình lôgarit sau: ln|x - 2| + ln|x + 4| ≤ 3ln2
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Giải các bất phương trình sau: (2x − 7)ln(x + 1) > 0
Giải bất phương trình ln (1 + x)< x ?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Biết I = ∫ 1 3 3 + ln x ( x + 1 ) 2 d x = a ( 1 + ln 3 ) - b ln 2 . Khi đó a 2 + b 2 bằng:
A. a 2 + b 2 = 7 16
B. a 2 + b 2 = 16 9
C. a 2 + b 2 = 25 16
D. a 2 + b 2 = 3 4
Tìm số nghiệm của phương trình ln ( x ) + ln ( 2 x - 1 ) = 0
A. 2
B. 4
C. 1
D. 0
Số nghiệm của phương trình ln x + ln(3x – 2) = 0 là?
A. 1.
B. 3.
C. 0.
D. 2.
Tìm miền xác định của hàm số y = ln(ln(lnx))
A. D = (0; +∞)
B. D = (1; +∞)
C. D = (e; +∞)
D. D = ( e e ; + ∞ )