Question

Giải các phương trình:

a ) ( x + 3 ) ( x − 3 ) 3 + 2 = x ( 1 − x ) b ) x + 2 x − 5 + 3 = 6 2 − x c ) 4 x + 1 = − x 2 − x + 2 ( x + 1 ) ( x + 2 )

Answer 1

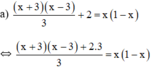
⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)

⇔ x 2 − 9 + 6 = 3 x − 3 x 2 ⇔ x 2 − 9 + 6 − 3 x + 3 x 2 = 0 ⇔ 4 x 2 − 3 x − 3 = 0

Có a = 4; b = -3; c = -3  ⇒   Δ   =   ( - 3 ) 2   –   4 . 4 . ( - 3 )   =   57   >   0

Phương trình có hai nghiệm

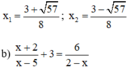
Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được :

(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)

⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x = 6 x − 30 ⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x − 6 x + 30 = 0 ⇔ − 4 x 2 + 15 x + 4 = 0

Có a = -4; b = 15; c = 4  ⇒   Δ   =   15 2   –   4 . ( - 4 ) . 4   =   289   >   0

Phương trình có hai nghiệm phân biệt:

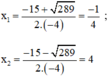
Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm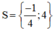 

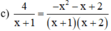
Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

4 ⋅ ( x + 2 ) = − x 2 − x + 2 ⇔ 4 x + 8 = − x 2 − x + 2 ⇔ 4 x + 8 + x 2 + x − 2 = 0 ⇔ x 2 + 5 x + 6 = 0

Có a = 1; b = 5; c = 6  ⇒   Δ   =   5 2   –   4 . 1 . 6   =   1   >   0

⇒ Phương trình có hai nghiệm phân biệt:

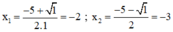
Chỉ có nghiệm x 2   =   - 3  thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.