Ta có: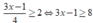 ⇔ 3x - 1 > 8
⇔ 3x - 1 > 8
⇔ 3x ≥ 9 ⇔ x ≥ 3
Vậy x ≥ 3 là nghiệm của bất phương trình.
Ta biểu diễn tập nghiệm trên trục số như sau:
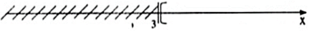
Ta có: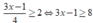 ⇔ 3x - 1 > 8
⇔ 3x - 1 > 8
⇔ 3x ≥ 9 ⇔ x ≥ 3
Vậy x ≥ 3 là nghiệm của bất phương trình.
Ta biểu diễn tập nghiệm trên trục số như sau:
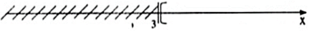
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
\(\dfrac{x-2}{2}+1\)≤\(\dfrac{x-1}{3}\)
Giải bất phương trình và biểu diễn tập nghiệm trên trục số
(x-2)(2x-3)+3(x+4)<2(x+1)2-4x
Giải bất phương trình sau và biểu diễn nghiệm trên trục số
x-2/6 - x-1/3 < x/2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số a)(4x-1)(x²+12)(-x+4)>0
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số x + 3 > 6
Giải bất phương trình và biểu diễn tập nghiệm trên trục số
\(\dfrac{x+4}{5}\) - \(\dfrac{x-2}{3}\) > 2
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) ( 2 x + 3 ) ( 2 x − 1 ) < ( 2 x − 5 ) 2
b) ( x − 1 ) ( x + 2 ) < ( x − 1 ) 2 + 3
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
\(\dfrac{1-2x}{4}-2< \dfrac{1-5x}{8}\)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 x + 2 3 < x + 4 ; b) 2 x − 5 ≥ − 2 x + 3
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x - 1 ≥ 5
b) x-2 /3 ≥ x - x-1 /2