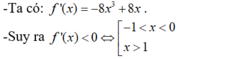Các câu hỏi tương tự
Giải bất phương trình:
2
x
f
(
x
)
≥
0
với
f
(
x
)
x
+
x
2
+
1
A.
x
≥
1
3
B.
x
1
3
C.
x
1...
Đọc tiếp
Giải bất phương trình: 2 x f ' ( x ) ≥ 0 với f ( x ) = x + x 2 + 1
A. x ≥ 1 3
B. x > 1 3
C. x < 1 3
D. x ≥ 2 3
Giải bất phương trình
f
(
x
)
≥
0
với
f
(
x
)
2
x
3
-
3
x
2
+
1
A.
x
≤
0
x
≥
1
B. ...
Đọc tiếp
Giải bất phương trình f ' ( x ) ≥ 0 với f ( x ) = 2 x 3 - 3 x 2 + 1
A. x ≤ 0 x ≥ 1
B. x ≤ 1
C. x ≥ 0
D. 0 ≤ x ≤ 1
Giải bất phương trình f(x) 0 với
f
(
x
)
-
2
x
4
+
4
x
2
+
1
A.
-
1
x
0
x
1...
Đọc tiếp
Giải bất phương trình f'(x) < 0 với f ( x ) = - 2 x 4 + 4 x 2 + 1
A. - 1 < x < 0 x > 1
B. -1 < x < 0
C. x > 1
D. x < 0
Giải bất phương trình
f
(
x
)
≥
0
với
f
(
x
)
2
x
3
−
3
x
2
+
1
A.
x
≤
0
h
o
ặ
c
x
≥
1
B....
Đọc tiếp
Giải bất phương trình f ' ( x ) ≥ 0 với f ( x ) = 2 x 3 − 3 x 2 + 1
A. x ≤ 0 h o ặ c x ≥ 1
B. x ≤ 1
C. x ≥ 0
D. 0 ≤ x ≤ 1
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1
Cho hàm số y= f(x)=x^3-2x^2 (C) a) Tìm f'(x). Giải bất phương trình f'(x)>0 b) Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Cho hàm số y = f(x)=x^3-2x^2(C) a) tìm f'(x) . Giải bất phương trình f'(x)>0 b) viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Cho hàm số
f
(
x
x
3
+
b
x
2
+
c
x
+
d
,
C
g
x
x
2
-
3
x
+
1
Với các số b, c, d tìm được ở bài 19, hãy:a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ...
Đọc tiếp
Cho hàm số f ( x = x 3 + b x 2 + c x + d , C g x = x 2 - 3 x + 1
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = - 1 .
b) Giải phương trình f ' sin x = 0 .
c) tính lim x → 0 f ' ' sin 5 x + 1 g ' sin 3 x + 3